ESTADÍSTICA INFERENCIAL VS. DESCRIPTIVA

Descriptiva	Inferencial
Refiere a los procedimientos empleados para organizar y resumir conjuntos de observaciones en forma cuantitativa de la totalidad de individuos de una población Reducción de datos cuantitativos a un pequeño número de términos descriptivos que representan observaciones estadística aplicables a mi muestra. No pueden generalizarse los resultado de una muestra a la población.	Refiere a los métodos empleados para inferir algo acerca de una población (apoyada en el cálculo de las probabilidades), basándose en los datos obtenidos a partir de una muestra. Los métodos de la estadística inferencial nos señalan los procedimientos que tenemos que seguir para extraer conclusiones válidas y confiables a partir de la evidencia de las muestras.

ASOCIACIÓN ENTRE VARIABLES

La forma en la que se relacionan dos variables se denomina asociación entre variables. La relación entre dos variables puede caracterizarse mediante el estudio de la existencia de la asociación, lafuerza, la dirección y su naturaleza.

Asociación: existe asociación entre dos variables cuando la distribución de una variable difiere entre las diversas categorías de la segunda variable.

-Épsilon: es una forma de calcular asociación y resulta de las diferencias porcentuales, cuando épsilon mayor a O quiere decir que hay asociación.

-Delta: se basa en la comparación entre frecuencias observadas en una tabla con las frecuencias esperadas, es decir un modelo de no asociación. Delta no puede medir la fuerza de la asociación, ya que el mismo no se encuentra estandarizado, no presenta un valor máximo y mínimo entre los que puede variar los deltas obtenidos.

Para sacar frecuencias esperadas hacer:

	I	II	TOTAL
I	A	B	52
II	C	D	40
TOTAL	30	62	92

A observada= 52 x 30/92= 16.9

C observada= 40 x30/92= 13

Cuanto más se alejen las frecuencias observadas de las esperadas, más asociación. Los valores altos de la sumatoria de Delta indicaran un alto nivel de asociación y viceversa. Si la sumatoria de Delta es igual a cero, no hay asociación

Fuerza: los coeficientes de asociación son medidas estandarizadas que indican un valor mínimo y un valor máximo, incluyendo en algunos casos otra categoría que muestra la ausencia de asociación (pueden ir de -1 a 1 o de 0 a 1). La propiedad de contar con valores estandarizados posibilita la comparación de valores obtenidos en diferentes tablas de asociación, estableciendo las diferencias y similitudes en lo que respecta a la fuerza de las asociaciones: a mayor coeficiente, mayor fuerza de asociación.

Dirección: la interpretación del valor obtenido nos permite determinar si la dirección de la asociación es positiva (+1) o negativa (-1) siempre y cuando las variables hayan sido medidas mínimamente a nivel ordinal, dado que puede observarse el grado en que aumentan o disminuyen los valores de una variable en función de la otra. La correspondencia entre los valores altos de las dos variables y viceversa indica que hay una asociación positiva (a mayor tanto mayor tanto, a menor tanto menor tanto), en tanto la correspondencia entre los valores altos de una variable y los bajos de la otra dan cuenta de una asociación negativa o inversa.

Naturaleza: la naturaleza está indicada por la forma en la que se distribuyen los datos en una tabla o en el trazado de una recta en la representación gráfica. En el caso de los datos presentado en tablas se habla de asociación perfecta cuando todos los casos se agrupan en una diagonal, lo que significa que cada valor de una variable se encuentra asociada con un solo valor de la segunda variable, de tal modo que para cualquier categoría de la variable independiente, sólo será diferente de 0 una celdilla de la variable dependiente mientras que el resto de las celdillas serán 0. Se produce una asociación lineal cuando los datos se concentran en la variable dependiente siguiendo una línea recta. La distribución es irregular cuando se distribuye aleatoriamente. En términos de la representación gráfica, la asociación perfecta positiva tendrá una recta positiva y creciente, mientras que la asociación perfecta negativa tendrá una pendiente negativa y decreciente.

En el gráfico de dispersión, la fuerza de la correlación entre X e Y, incrementa a medida que los puntos en el diagrama se acercan más a una línea diagonal imaginaria.

Existen dos clases de pruebas estadísticas para medir la asociación entre dos variables: las paramétricas y las no paramétricas. Las paramétricas tienen mayor capacidad detectar una relación real entre dos variables. Exigen que los datos cumplan tres requisitos: 1) que la variable dependiente sea por lo menos intervalar (numérica) 2) que los valores de la variable dependiente sigan una distribución normal y 3) que las varianzas de la variable dependiente en los grupos sean aproximadamente iguales. Para el estudio de la asociación entre variables nominal y ordinal se utilizan pruebas estadísticas no paramétricas.

Cuando trabajamos con variables intervalares, la medición de la asociación puede ser más precisa ya que podemos tener en cuenta las distancias que existen entre los valores de las variables. Es por eso, que podemos calcular la correlación entre variables intervalares: los valores de una de ella, varía en forma sistemática con respecto a los valores homónimos de los otros.

COEFICIENTES

Criterios a tener cuenta para la elección de coeficientes:

- Nivel de medición

-Las medidas de asociación pueden agruparse en dos grandes grupos: aquellas diseñadas para analizar relaciones simétricas (no requieren que se distingan previamente la variable dependiente de la independiente).

-Tipo de hipótesis: diagonal/rinconal. Las diagonales estudian cómo se distribuyen los casos en una diagonal y en la rinconal sólo se considera una variable (los coeficientes que se pueden utilizar para hipótesis diagonal, también se pueden aplicar a las rinconales pero no al revés)

-Cantidad de categorías de la variables (tamaño de la tabla).

-Los coeficientes pueden estar basados en chi cuadrado o en la reducción proporcional del error (RPE)

Chi – cuadrado : se saca elevando los deltas al cuadrado y dividendo cada uno de ellos por su frecuencia esperada, esos resultados los sumas y te dan chi cuadrado. No es una medida estandarizada. Compara las FO con las Fe en caso de que no existiera asociación entre ellas. Es siempre un numero positivo. Evalúa si existe algún tipo de dependencia entre los valores de dos o mas variable observadas. COPIAR FÓRMULA.

Reducción proporcional del error: la lógica de estos coeficiente opera en función de cuánto mejoraría la predicción de la variable dependiente una vez que conozco la distribución de la variable independiente. Los coeficientes basados en la reducción proporcional del error operan a partir de dos predicciones diferentes sobre los valores que asumen los casos. En la primera predicción se conoce la info sobre la distribución de la variable dependiente pero se ignora la información sobre la variable independiente. En la segunda predicción se toma en cuenta el valor de los casos en la variable independiente para predecir su valor en la variable dependiente. Con esta información, los coeficientes estiman qué proporción se reduce el error cometido en al primera predicción cuando dispongo la información de la segunda predicción. Si las variables no estuvieran asociadas, no mejoraría en nada mi predicción pero si hubiera asociación acertaría en un mayor porcentaje de casos conociendo la distribución de la variable dependiente en otra variable. Cuanto mayor sea la proporción del error que se reduce en la predicción de la variable dependiente, mayor será la asociación entre las dos variables.

En variables nominales indican la existencia y la fuerza de la asociación. En variables ordinales indican además la dirección de la asociación entre la asociación

CORRELACIÓN

Fuerza: el grado de correlación varía respecto a su fuerza. Estas diferencias se pueden visualizar en la fuerza de la correlación por medio de un diagrama de dispersión, que muestra la forma en que los puntajes de dos variables cualquiera están dispersos en toda la escala de los posibles valores de los puntajes. La fuerza de la correlación entre X e Y aumenta a medida que los puntos del diagrama de dispersión se estrechan formando una línea recta imaginaria (podemos identificar esa línea de regresión)

Dirección: la interpretación del valor obtenido nos permite determinar si la dirección de la asociación es positiva (+1) o negativa (-1) siempre y cuando las variables hayan sido medidas mínimamente a nivel ordinal, dado que puede observarse el grado en que aumentan o disminuyen los valores de una variable en función de la otra. La correspondencia entre los valores altos de las dos variables y viceversa indica que hay una asociación positiva (a mayor tanto mayor tanto, a menor tanto menor tanto), en tanto la correspondencia entre los valores altos de una variable y los bajos de la otra dan cuenta de una asociación negativa o inversa.

Gráficos lineales vs curvilineales

Cuando es positiva o negativa, la correlación es lineal. Existen a su vez, muchas correlaciones curvilíneas que indican que una variable aumenta a medida que la otra se incrementa hasta que la relación misma se invierta, de manera que una variable decrece mientras que la otra sigue acrecentándose. O sea que una relación que empieza como positiva se vuelve como negativa y viceversa. Ejemplo: las familias de clase media tienen un número pequeño de hijos, el tamaño de la familia aumenta a media que el estatus socioeconómico se vuelve más alto y más bajo.

Regresión (solo para intervalar)

Establecer una correlación entre dos variables puede ser útil para predecir los valores de una variable Y conociendo los valores de la variable X. La técnica que se emplea para hacer tal predicción se conoce como análisis de regresión.

La forma que más se utiliza en la práctica es la relación lineal. La ecuación matemática se denomina función lineal de la regresión y se expresa:

Donde:

a= es la intersección de y (el valor esperado de y cuando x = 0). También se conoce como ordenada del origen.

b= curva o coeficiente de regresión para X. Representa la cantidad esperada de cambio de y (ascenso o descenso) para cada cambio de una unidad de la variable x. Se la denomina pendiente de la recta.

e= término de error o término de disturbio.

En el análisis de regresión es central observar que parte de la variación total en Y se debe a la variación total en X y cuanto de la variación de Y no explica X.

La regresión simple solo considera una variable dependiente y una variable independiente.

La regresión múltiple considera dos o más variables independientes. Y permite comparar diferentes modelos de regresión y cuáles de ellos predicen mejor el comportamiento de la variable dependiente en relación con un grupo de variables independientes.

R de Pearsons es el coeficiente que se utiliza para analizar la correlación entre variables intervalares.

ESTADÍSTICA INFERENCIAL

CURVA NORMAL

Las distribuciones de frecuencia pueden tomar distintas formas: pueden ser simétricas o estar sesgadas ya sea positivamente o negativamente, tener más de una joroba, etc (no todos los fenómenos se distribuyen normalmente).

La curva normal es un tipo de distribución simétrica. Puede utilizarse para describir distribuciones de puntajes, para interpretar la desviación estándar y para hacer un informe de probabilidades.

Características de la curva normal:

-Simétrica: si doblamos la curva en su punto más alto al centro, crearíamos dos mitades iguales (esto es así porque la media se ubica en ese punto máximo).

-Unimodal: solo tiene un pico o punto de máxima frecuencia que es aquel punto en la mitad de la curva en el cual coinciden la moda, la media y la mediana.

-Asintótica: desde el pico central de la distribución normal, la curva cae gradualmente en ambas colas, extendiéndose indefinidamente en ambas direcciones acercándose cada vez más a la línea de base sin alcanzarla realmente.

La curva normal es sólo para variables numéricas, es decir intervalares. Cada distribución normal tiene una media y desviación estándar propia. La desviación estándar determina el grado de apuntamiento de la curva, cuanto mayor sea el valor de la desviación más se dispersarán los datos en torno a la media y la curva será más plana.

En la distribución normal se corre el origen, que pasa a ser la media. Todas las medidas se miden con desvíos respecto a la media.

El área bajo de la curva normal es aquella área que está entre la curva y la línea base y que contiene el 100% de los casos en una distribución normal dada.

Una proporción constante del área total bajo la curva normal, estará entre la media y cualquier distancia dada de X, medida en unidades. Así el área bajo la curva normal entre la media y el punto 1 DE arriba de la media incluye siempre el 34,13% total de casos, independientemente de que estemos estudiando.

La naturaleza simétrica de la curva normal hace que cualquier distancia x dada arriba de la media contiene una proporción idéntica de casos que la misma distancia x por debajo de la media: el área entre la media y 1 desviación estándar para arriba es 34,13%, lo mismo que entre la media y 1 desviación estándar para abajo.

-Entre – 1DE y + 1 DE están comprendido el 68,26% del área total.

-Entre – 2 DE y + 2 DE están el 95,44% (47,72 + 47,72)

-Entre – 3 DE y + 3 DE están el 99,74 % (49,87 + 49,87) – incluyen prácticamente todos los casos bajo cualquier distribución normal.

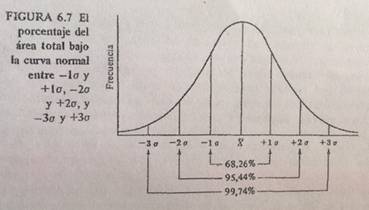
Una importante función de la curva normal es la aclaración del significado de la desviación estándar.

Conociendo la desviación estándar de cada conjunto de puntajes de coeficiente intelectual y suponiendo que cada conjunto está distribuido normalmente podríamos estimar y comparar el porcentaje de hombres y mujeres que tienen cualquier extensión de puntajes de coeficiente intelectual.

¿Cómo resolver un ejercicio?

Paso 0: dibujar la curva normal para la variable, sombrear el área designada desde la media hasta la puntuación x especificada.

1er paso: convertimos un puntaje crudo en unidades de DE dividiendo la distancia entre éste y la media entre la DE. Puntaje z o estándar indica la dirección y el grado en que cualquier puntaje crudo se desvía de la media de una distribución en una escala de unidades DE.

(el resultado puede ser positivo o negativo dependiendo de si una puntuación bruta está arriba o debajo de la media).

2do paso: usando la tabla de puntajes z --- localizo el puntaje z y hallo el porcentaje que le corresponde. La tabla de puntajes z muestra el área desde la media hasta una puntuación z.

Ejemplo de cómo resolver un problema más complejo:

-Si te piden encontrar la proporción de casos mayores que una puntuación Z, lo que hay que hacer es restarle al 50% el porcentaje que le corresponda a esa puntuación Z.

-Si te piden encontrar la proporción de casos comprendidos entre dos puntos (uno positivo y otro negativo) sumas la proporción de cada uno en función de la media.

-En caso de que haya dos puntuaciones de un mismo lado de la media, se le resta a la proporción del puntaje z más alto el más bajo.

-Para sacar los casos menores que una puntuación X mayor que la media, sacas el porcentaje que le corresponde a esa puntuación z y le sumas el 50%.

Puntuaciones z críticas

Existen ciertas puntuaciones z y áreas bajo la curva normal que son de gran importancia en los procedimientos estadísticos y que se usan con frecuencia. Estas zonas se llaman puntuaciones z críticas. Las regiones críticas son áreas bajo la curva que se ven como probabilidades (alfa). Son decisivas al determinar el grado de confianza que asignamos a nuestros resultados reportados.

La puntuación z crítica más frecuentemente usada es +/- 96. 95% del área bajo una curva normal cae entre +1,96 y -1,96 dejando 5% del área distribuida en las dos colas (2,5% en las dos colas).

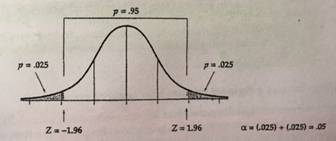
Las áreas bajo la curva normal representan probabilidades de ocurrencia. Dentro de una curva normal, la probabilidad disminuye a medida que nos alejamos de la media.

PROBABILIAD

Una probabilidad es una especificación de que tan frecuente es probable que ocurra un evento de interés particular entre un gran número de ensayos. Llamamos probabilidad de éxito, a la probabilidad de ocurrencia de este evento de interés así como la probabilidad de fracaso es la probabilidad de que no ocurra el evento.

P (de éxito) = resultados exitosos posibles/total de resultados posibles

Las probabilidades pueden presentarse también como porcentajes, multiplicando p x 100.

Reglas básicas

1) Las probabilidades oscilan entre 0 y 1.

2) La regla de adición para eventos alternativos: la probabilidad de eventos alternativo es igual a la suma de las probabilidades de los eventos individuales. La probabilidad de que salga un rey o un as en un maso de cartas es igual probabilidad de rey + probabilidad de as.

3) Ajusta para las ocurrencias conjuntas: cuando tenemos un evento que tiene doble éxito, la probabilidad de que salga rey o reina o corazón no es p rey + p reina + corazón porque rey y reina tienen corazón. Entonces le restamos la ocurrencia conjunta. Fórmula final: p (rey) + p (reina) + p (corazón) – p (ocurrencias conjuntas) que en este caso 2/total de cartas.

4) Regla multiplicativa para eventos compuestos. Señala que la probabilidad de un evento compuesto (con partes múltiples) es igual al múltiplo de las probabilidades de las partes separadas del evento.

5) Explicación del reemplazamiento con eventos compuestos.

MODELOS EXPLICATIVOS

Ideográfico: este modelos pretende proporcionar una explicación mediante la enumeración de las consideraciones abundantes. Ejemplo: historiadores enumeran todas las causas peculiares de la revolución francesa.

Nomotético: este modelos no enumera todos los elementos sino que revelas las consideraciones más importantes para explicar los sucesos. Este modelo pretende dar la explicación más amplia con el menor número de variables causales para descubrir esquemas generales de causa y efecto. Inevitablemente este modelo es probabilístico en esta forma de abordar la causalidad. El modelo indica una probabilidad muy alta o muy baja de que ocurra cierta acción cada vez que un número limitado de consideraciones específicas está presente.

Lo más útil para la investigación social es combinar los dos métodos.

Lazarsfeld propuso tres criterios de causalidad entre las variables para la explicación nomotética:

1- La causa debe preceder en el tiempo al efecto

2- Las dos variables deben guardar una relación empírica (aunque hay pocas correlaciones que son perfectas).

3- La correlación empírica observada entre dos variables no puede explicarse por una tercera variable que sea la causa de ambas.

Una causa necesaria representa una condición que debe estar presente para que el efecto se produzca. Una causa suficiente representa una condición que si, esta presente, garantiza en gran medida el efecto en cuestión. Cuando analizamos las relaciones nomotéticas entre variables nunca descubrimos causas únicas que sean absolutamente necesarias y absolutamente suficientes. En las ciencias sociales, las causas necesarias o suficientes pueden ser la base para concluir que existe una relación causal.

En el caso del pensamiento científico, empleamos la expresión razonamiento critico para referirnos a nuestro interés en evitar los errores comunes de los razonamientos cotidianos. A veces es posible detectar fallos en el razonamiento causal exclusivamente sobre las bases lógicas: cuando no es posible examinar los datos empíricos.

MUESTRAS

Por diversas limitaciones, el investigador analiza sólo una muestra: un número pequeño de individuos tomado de alguna población. A través del proceso de muestreo, el investigador social busca generalizar de su muestra a la totalidad de la población de donde la obtuvo. Para hacer tales inferencias, el investigador escoge un método de muestreo apropiado para ver si todos los miembros de la muestra tienen igual oportunidad de ser integrados en ella. Si a cada miembro de la población se le da igual oportunidad de ser escogido para la muestra se esta utilizando un método aleatorio, de no ser así, el método empleado es no – aleatorio.

Etapas en la selección de una muestra:

1-Definición de la población objetivo en términos de contenido, unidades, extensión y tiempo.

2-Identificar el marco muestral (solo para probabilísticas)

3-Determinar el método de muestreo.

4-Determinar el tamaño de la muestra considerando factores cualitativos: importancia de la decisión, naturaleza de la investigación, el número de variables, la naturaleza del análisis, las restricciones de recursos, el tamaño de muestra utilizado en estudios similares. En universos muy heterogéneos, la muestra tiene que ser mayor que universos más homogéneos.

Muestras no aleatorias

-Muestreo por accidente: El investigador simplemente incluye los casos más convenientes en su muestra y excluye de ella los casos inconvenientes.

-Muestreo por cuotas: las diversas características de una población tales como edad, sexo, clase social, son muestreadas de acuerdo con el porcentaje que ocupan dentro de la población. En cuanto a las variables que se utilizan para las cuotas, no caben muchas alternativas ya que suele existir información escasa sobre el universo objeto de estudio. Por eso casi siempre se introducen las cuotas de sexo y edad. El muestreo por cuota no es generalizable pero si representativo y suele usarse en la investigación social.

-Muestreo intencional o de juicio: la lógica o el sentido común se usan para seleccionar una muestra que sea representativa.

Muestras aleatorias

La inferencia estadística implica extraer conclusiones sobre una población con base en los estadísticos de una muestra. Las inferencias estadísticas deben tomar en cuenta el error de muestreo. En muestras probabilísticas conozco el error de muestreo, lo que me permite discernir si los efectos estadísticos observados son reales en la población o simplemente resultado del error de muestreo. Conoces los intervalos de confianza y de riesgo.

En las muestras probabilísticas cada elemento del universo tiene una probabilidad igual e independiente de figurar en la muestra. Esta característica del muestreo aleatorio indica que cada miembro de la población debe ser identificado antes de obtener dicha muestra aleatoria, requisito que generalmente se llena obteniendo una lista que incluya a todos y cada uno de los miembros (marco muestral).

En este supuesto las estimaciones son insesgadas (esto equivale a afirmar la coincidencia de la media del muestreo con la de la población) y se pueden calcular los errores de muestreo que permiten determinar la precisión de las estimaciones. La precisión hace referencia a la concentración de valores en el muestreo, es decir a la poca variabilidad.

En una encuesta muestral, en unos casos se puede hablar de estimaciones en otros de tendencias y en muchos de nada, ya que los errores son muy elevados. Cuando el intervalo de confianza en que se sitúa la estimación es muy amplio, el valor de la estimación es escaso.

Muestreo aleatorio simple: la selección de los elementos de la muestra se realizar en una sola etapa y directamente al azar. Se suelen usar tablas de números aleatorios. Para ello el investigador social obtiene primero su lista de la población y le asigna un número de identificación único a todos y cada uno de sus miembros. Habiendo preparado la lista, procede a sacar los miembros de una muestra de una tabla de números aleatorios. Una tabla de números aleatorios se construye de forma tal que genere serie de números sin ningún patrón u orden determinado.

Todos los métodos de muestreo aleatorio son en realidad variaciones del procedimiento de muestreo simple.

Muestreo sistemático: no se requiere tabla de números aleatorios, ya que se hace el muestreo con una lista de miembros de la población por intervalos fijos. Como resultado este método es más rápido que el anterior pero se corre el riesgo de que se seleccione más de una vez a ciertos miembros de la población, mientras que otros no se seleccionan. A su vez, si el listado esta ordenado en base a un criterio (ejemplo: primero hombres, luego mujeres) no rige la aleatoriedad.

Este tipo de muestreo requiere de un criterio de ordenamiento de las unidades de análisis para evitar el sesgo de selección de periodicidad constante.

Muestreo estratificado: se definen previamente grupos o subgrupos (estratos) que deben ser diferentes entre si pero homogéneos en su interior. Habiendo identificado nuestros estratos, procedemos a tomar una muestra aleatoria simple de cada subgrupo o estrato hasta que hayamos muestrado a toda población. La estratificación se basa en la idea de que un grupo homogéneo requiere una muestra más pequeña que un grupo heterogéneo. El investigador decidirá las variables que va a utilizar para estratificar y el número de estratos resultantes. Los estratos pueden ser proporcionales o no con respecto a la población que se estudia, si bien por lo genera es de tipo proporcionar. Este tipo de muestra es conveniente cuando la población puede ser divida en categorías que tienen un interés analítico y que por razones teóricas y/o empíricas presentan diferencias entre ellas.

Mientras que los miembros de las muestras por cuotas se toman por cualquier método que escoge el investigador, los miembros de las muestras estratificadas se seleccionan siempre sobre una base aleatorio, generalmente la simple.

Muestra aleatoria por conglomerados: la unidad muestral no son los individuos sino un conjunto de ellos que bajo determinados aspectos se puede considerar que forman una unidad (unidades hospitalarias, departamentos universitarios). Los conglomerados deben ser iguales entre sí y heterogéneos en su interior. Definidas las unidades muestrales, la forma de operar para extraer la muestra depende del tamaño del mismo. Cuando este es pequeño se puede proceder de forma similar a la señalada en los epígrafes pero entrevistando a todos los elementos del conglomerado. Si estos son muy grandes, resulta imposible la aplicación de las entrevistado a todos los elementos por lo que hay que recurrir al submuestreo.

-El muestreo por conglomerados monoetápico, consta de la aplicación de los muestreos aleatorio simple, sistemático o estratificado pero tomando como unidad de muestreo los conglomerados.

-El muestreo por conglomerados polietápico: se divide en un cierto número de unidades más pequeñas las unidades muestrales, es decir que la unidad final de muestreo no son los conglomerados sino subdivisiones de estos.

Error de muestreo

Para valorar el grado de validez de una inferencia, es preciso indicar algunas características esenciales de las muestras: errores contemplados, tamaños de la muestra, intervalo de confianza.

Siempre podemos esperar que haya una diferencia entre una muestra y la población de la que se ha extraído. La media y la desviación estándar de la muestra casi nunca serán exactamente igual a la media y la DE de la población. Esta diferencia, conocida como error de muestreo, surge sin importar que tan bien se haya diseñado, realizado el plan de muestreo.

Dada la presencia del error de muestreo, mediante la distribución muestral de medias es posible a partir de una muestra aleatoria realizar generalizaciones a la población. Idealmente es una distribución de frecuencia de una gran número de medias de muestras aleatorias que se han extraído de la misma población. Para poder construir esta distribución, primero tendríamos que sacar muchas muestras aleatorias de nuestra población, calcular la media de cada una de ellas, construir una distribución de frecuencias de dichas medias, sacar el promedio (la media) y compararlo con el de la población.

Características de la DMM:

-Se aproxima a una curva normal por lo tanto se vale de las propiedades de la curva normal. Podemos encontrar la probabilidad de obtener puntajes crudos en una distribución dadas una cierta media y su DE. Dado que la distribución muestral toma la forma de la curva normal, podemos usar también los puntajes z y la tabla para tener la probabilidad de cualquier media muestral. El hecho de que la DMM este normalmente distribuida implica que el 99% de las medias de las posibles muestras van a caer dentro de los seis desvíos estándar.

-La media de la DMM es igual a la media de la población.

-La desviación estándar de una DMM es menor que la DE de la población. Esto es así ya que tomamos datos medios, eliminando así los valores de puntajes crudos extremos.

El teorema del límite central es el fundamento matemático que garantiza una distribución normal cuando el tamaño de la muestra es suficientemente grande.

Error estándar de la media

El investigador social no tiene un conocimiento real sobre la media de medias o la desviación estándar de la distribución maestral, sin embargo si puede estimar mediante el error estándar de la media, la desviación estándar de la distribución muestral de medias sobre la base de los datos recogidos en una sola muestra. Con la ayuda del error estándar de la media, podemos encontrar el rango de valores de la media dentro del cual es probable que fluctué nuestra verdadera media poblacional.

El intervalo de confianza también nos permite estimar la probabilidad de que nuestra media poblacional caiga dentro de un rango de valores medios. Se determina a partir de los resultados de la muestra y el error de muestreo. Pueden construirse intervalos de confianza para cualquier nivel de probabilidad. Se ha convertido en una convención utilizar un intervalo de confianza más amplio, menos preciso que tiene mejores probabilidades de hacer una estimación exacta de la media poblacional: intervalo de confianza de 95%. Por medio de este se estima la media poblacional sabiendo que hay 95 oportunidades entre 100 de estar en lo ciento y cinco oportunidades de equivocarse. Para encontrar el intervalo de confianza de 95% debemos multiplicar primero el error estándar de la media x 1,96 (valor obtenido de la tabla z).

Intervalo de confianza del 95%= media +/- 1,96 x error estándar de la media.

Nivel de confianza: probabilidad de obtener un intervalo de confianza concreto o estimación determinada.

PONDERACIÓN DE MUESTRAS

Algunos estadísticos requieren emplear coeficientes de ponderación para asignar importancias diferentes a los valores de las variables una vez finalizada la recolección de los datos. Esta decisión suele tomarse al observar que ciertas variables principales (recogidas en el marco de una muestra que busca representatividad) presenta sesgos/ diferencias con los valores de la población de la que la muestra fue extraída y por lo tanto, ven afectada su validez externa si, además la muestra fue probabilística. Se pondera una muestra a partir de una distancia entre los valores de la población con los de la muestra recogida.

LAZARSFELD

Modelo de análisis de covarianzas que ofrece la posibilidad de incorporar un factor de control que especifica la hipótesis original. Este modelo define y establece asociación por oposición a la idea de independencia estadística y establece la fuerza de la relación entre dos variables de acuerdo a su lejanía o no respecto de la independencia estadística. Una vez elaborada la hipótesis principal, uno puede encontrarse con factores que están invalidando dicha relación. De manera que hay que controlar dichas variables. Al determinar cuáles serían las variables de control, uno formula hipótesis alternativas.

Se parte de una hipótesis nula que postula que no hay relación entre las variables si se puede rechazar esta hipótesis, entonces se puede aceptar la hipótesis alternativa que sostiene que existe asociación entre variables. Una vez elegida la prueba estadística más apropiada, se especifica el nivel de significación con el cual se rechazará la hipótesis nula, es decir, se determina la probabilidad de cometer error tipo 1 (aquel que se comete al rechazar una hipótesis nula siendo ésta verdadera)

Hay que determinar: qué coeficientes usar (justificándolo) y qué intervalo de confianza utilizaremos

Sí consideramos el orden temporal de las variables, la variable de control puede ser anterior a la variable independiente (X) o puede aparecer entre ésta y la variable dependiente. En el primer caso decimos que la relación es anterior y en el segundo, interviniente. La posición temporal está íntimamente relacionada con la teoría y no con cuestiones estadísticas.

Relación original= Relación parcial 1 (relación entre las variables X e Y en presencia del atributo T) + Relación parcial 2 (relación entre las variables X e Y en ausencia del atributo T) + Relación marginal 1 (relación entre la variable independiente y la de control) Relación marginal 2 (relación entre la variable dependiente y la de control)

De esta ecuación se pueden desprender dos situaciones:

a- Las relaciones marginales tienden a cero y las relaciones parciales son mayores que la original. Se trata de relaciones de tipo parcial. Si es importante distinguir cual de las dos relaciones parciales es más importante (aquella que tenga mayor coeficiente de asociación tendrá una asociación más fuerte). En este caso la relación original se especifica. Hay dos tipos de especificación que dependerán de la temporalidad de la variable de control con respecto a la independiente:

- Si la variable de control es anterior a la independiente, se llama relación parcial anterior y el tipo de especificación es condición. XY se da con más fuerza si T. También podría llamarse especificación, ya que una de las parciales será necesariamente mayor que la relación original, especificando cuando XY se da con más fuerza. Corresponde a una secuencia de tipo estímulo-disposición-respuesta, siendo el estímulo la variable X y el factor de prueba la disposición.

- Si la variable de control es posterior a la independiente (interviniente), el tipo de especificación es contingencia.

b- Las relaciones parciales desaparecen o tienden a cero (son menores que la relación original) y los valores mayores se encuentran en las relaciones marginales. En este caso, se trataría de una relación de tipo marginal. No es importante tener en cuenta cual de las dos es mas alta

- Si la variable de control antecede a la independiente, se habla de explicación. En este caso, la relación original es espuria, ya que las variaciones en X y en Y se explican por T. Los parciales tienden a cero y el resultado de la original aparece como el producto de dos relaciones marginales, por lo cual el interés pasa inmediatamente a la relación entre el factor de prueba y la variable dependiente.

- Cuando la variable de control es posterior a la independiente, se trata de una relación marginal interviniente, es decir, interpretación. Es decir, X y T se tienen que dar conjuntamente para que suceda Y. En una interpretación, la variable T está entre X e Y: si el atributo se mantiene constante, la relación entre X e Y tenderá a desaparecer

OCURRENCIA TEMPORAL
Variable de control	Parciales	Marginales
Antecedente	Especificación	Explicación
Interviniente	Contingencia	Interpretación

Para Lazarsfeld existe relación causal entre dos variables si, para cualquier factor de prueba antecedente, la relación entre X e Y no desaparece, por lo cual la relación original puede ser llamada “causal”.

Cosas a tener en cuenta:

· Hipótesis original: utilizar el verbo influye/condiciona. En la hipótesis original (y en la alternativa) hay que especificar de qué manera varían la independiente con respecto a la dependiente.

· Hipótesis alternativa: utilizar el verbo se especifica

· A cada cuadro hay que ponerle: Número, título y después de eso hacer una lectura

· En las lecturas, tengo que comparar los datos usando la palabra proporcionalmente, y no basta con poner “es mayor que” /”es menor que”, sino que tengo que poner el porcentaje que le corresponde a cada valor.

· Antes de plantear las relaciones marginales, tengo que decidir la temporalidad de la variable de control con respecto a la independiente (la dependiente será siempre la “ultima”), para ver cómo hacer el cuadro, es decir, cual será dependiente (filas) y cual independiente (columnas)

· Después de hacer la ecuación de Lazarsfeld debo especificar: si mi hipótesis se corrobora o no, si la relación es de tipo parcial o marginal, el orden temporal de las variables, qué tipo de relación es. Después de eso, la conclusión