Tiempo disponible: 2 horas y 50 minutos

Se pone a disposición de estudiantes 9.10 h.

Se entrega (en formato WORD) a través del mail de cátedra a las 12.00 h como máximo, indicando en subject: APELLIDO – RECUPERATORIO SEGUNDO PARCIAL -DIA DE COMISIÓN DE PRÁCTICOS

1. En el año 2019, el Servicio de Psicología de Niños de la UBA realizó un estudio sobre las características sociodemográficas y rendimiento escolar de los niños escolarizados de barrios carenciados del Partido de Avellaneda. A partir del siguiente cuadro:

a) Formule dos hipótesis: una para la relación original planteada y otra que integre tanto las variables de la relación original como la variable de control considerada. Señale el estatus que cumple cada una de las variables, su nivel de medición y su sistema de categorías.

b) Complete todos los pasos del análisis multivariado. Para ello, con la información suministrada elabore los cuadros correspondientes para poner a prueba las hipótesis, numérelos en el orden en que se analizarán, incluyendo sus títulos y fuentes correspondientes. Finalmente, interprete los resultados en función de las hipótesis formuladas utilizando porcentajes.

Situación de	Problemas				Edad del Padre
convivencia	de	Hasta 30 años			De 30 a 45 años			46 años o más	Total
de los padres	Aprendizaje
	Si
		230				330		105	665
vivien juntos	No
		274				426		84	784
	Total	504			756			189	1.449
	Si
			315		178			55	548
No viven
	No
		115				356		84	555
juntos
	Total	430			534			139	1.103

2. Responda si la siguiente proposición es VERDADERA o FALSA y justifique su respuesta recuperando la bibliografía sobre el tema:

“Si tengo un R de Pearson de 0,60 entre clase social y calidad del empleo, puedo decir que la clase social explica el 36% de la calidad del empleo”.

3. Un grupo de investigadores está comenzando un estudio cuantitativo sobre el impacto del programa de becas estudiantiles en reducir el abandono escolar y mejorar el compromiso con las tareas escolares. Para ello relevó una encuesta entre postulantes beneficiarios y no beneficiarios.

a) ¿Se podría utilizar para este estudio una muestra probabilística?

b) Si responde positivamente: ¿Qué tipo de muestra propondría y qué requerimientos de información disponible implicaría una muestra de ese tipo? Si responde negativamente: ¿Entonces qué tipo de muestra propondría?

Responda a la consigna recuperando la situación problemática planteada y la bibliografía.

1- a_ Relación Original: Los niños en edad escolar hijos de padres de hasta 30 años tenderían más a tener problemas en el aprendizaje que los hijos de padres de 30 a 45 años y los de 46 años o más.

Relación Parcial: Los niños en edad escolar hijos de padres de hasta 30 años tenderían más a tener problemas en el aprendizaje que los hijos de padres de 30 a 45 años y los de 46 años o más. Esta tendencia se invertiría en los hijos de padres de hasta 30 años cuyos padres viven juntos, a saber: los hijos de padres de hasta 30 años que viven juntos tendrían una menor probabilidad de presentar problemas en el aprendizaje que los hijos de padres de hasta 30 años que no viven juntos.

VI: Edad del Padre= Nivel de medición intervalar (Hasta 30 años; de 30 a 45 años; 46 años o más)

VD: Problemas de aprendizaje= Nivel de medición Nominal (Si ; No)

VC: Situación de convivencia de los padres= Nivel de medición Nominal (Viven Juntos ; No Viven Juntos)

b_ Cuadro 1: Problemas de aprendizaje según edad del padre. Avellaneda, 2019. -En porcentajes-

Fuente: Servicio de Psicología de Niños UBA

En el cuadro 1, nuestra relación original, si observamos en la categoría de Si de la variable Problemas de aprendizaje, notamos la gran diferencia porcentual entre hijos de padres de Hasta 30 años con las demás categorías de la variable edad del padre. Vemos un pronunciado 58.35 puntos porcentuales contra un 39.38 puntos porcentuales y 48.78 puntos porcentuales en padres de30 a 35 años y 46 años o más, respectivamente. Una diferencia de hasta casi 20 puntos con el primero y una diferencia de 10 puntos con el segundo. La presencia de problemas de aprendizaje en hijos cuyos padres tienen hasta 30 años, en comparación a las demás categorías de edad del padre, es evidente.

Al observar la categoría No de la variable Problemas de aprendizaje, con un 60.62%, los hijos cuyos padres tienen de 30 a 35 años se imponen frente a las demás categorías. A esta le sigue la categoría 46 años o más con un 51.22% y, fnalmente, los hijos de padres de hasta 30 años con un 41.65%, siendo estos últimos los que menos porcentaje para no presentar problemas en el aprendizaje tienen.

Cuadro 2 Problemas de aprendizaje según Edad del padre y según Situación de convivencia de los padres. Avellaneda 2019 -En porcentajes-

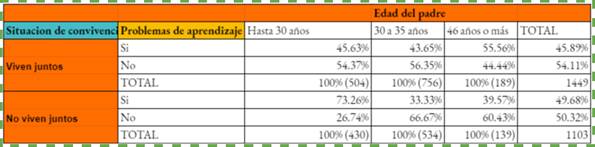
Fuente: Servicio de Psicología de Niños UBA

Al observar el cuadro 2, la relación parcial, notamos en la variable situación de convivencia, la categoría de padres que viven juntos, cuyos hijos Si presentan problemas de aprendizaje, los de 46 años o más, se imponen con un 55%, llevando una diferencia porcentual de 10 puntos en comparación a hasta 30 años y 30 a 35 años. Esto nos indica que en esta categoría, nuestra hipótesis original bivariada no se mantiene. Por otro lado, los hijos que No presentan problemas de aprendizaje de padres que viven juntos, son más numerosos en padres de 30 a 35 años con un 56%, siguiéndoles hasta 30 años con un 54.37% y, fnalizando con 46 años o más con un 44.44%.

En la categoría de padres que No viven juntos, cuyos hijos Si presentan problemas de aprendizaje, la categoría de hasta 30 años se impone con un 73.26% manteniendo la tendencia de nuestra relación original. Le siguen la categoría de 46 años o más con un 37.57% y, por último, 30 a 35 años, con un 33.33%. Una diferencia de 36 y 40 puntos porcentuales respectivamente si los comparamos a los hijos de padres de hasta 30 años. Por otro lado, en los hijos que No presentan problemas de aprendizaje de padres que no viven juntos, son más numerosos los padres de 30 a 35 años con un 66.67%, seguidos por 46 años o más con un 60.43% y, por último, hasta 30 años con un pobre 26.74%

Si seguimos observando el cuadro 2, vemos que nuestra tendencia a que los hijos cuyos padres presentan una edad de hasta 30 años tuviesen más problemas de aprendizaje, al introducir nuestra variable de control, situación de convivencia, solo se ve plasmada en la categoría de No viven juntos. Es más, pareciera que, al fnal, esta relación se profundiza en esta categoría, siendo un 58.35% en el cuadro 1 contra un 73.26% en el cuadro 2 viendo a los hijos cuyos padres son de hasta 30 años y no viven juntos.

3- Un grupo de investigadores está comenzando un estudio cuantitativo sobre el impacto del

programa de becas estudiantiles en reducir el abandono escolar y mejorar el compromiso con las

tareas escolares. Para ello relevó una encuesta entre postulantes beneficiarios y no beneficiarios.

a- ¿Se podría utilizar para este estudio una muestra probabilística? b- Si responde positivamente: ¿Qué tipo de muestra propondría y qué requerimientos de información disponible implicaría una muestra de ese tipo? Si responde negativamente: ¿Entonces qué tipo de muestra propondría?

Responda a la consigna recuperando la situación problemática planteada y la bibliografía.

A- Si, se podría utilizar una muestra probabilística.

B- En el caso de querer hacer este tipo de estudio, donde el marco muestral es accesible, es decir, una lista donde se presenten todas las unidades de análisis, es preferible hacer un muestreo del tipo estratifcado para una posterior elección de las unidades de análisis a partir de un muestreo simple o sistemático. ¿Por qué resulta accesible este marco muestral específco? Pues, siendo nuestro universo de estudio alumnos postulantes de becas estudiantiles, estos deberían de fgurar en un listado dado donde previamente se inscribieron para ser potenciales benefciarios de la beca (Supongamos que el programa de becas mencionado es uno específco y se busca conocer el impacto de dicha beca únicamente y no del groso de diferentes becas existentes en el país con distintos postulantes y benefciarios).

En fn, para nuestro muestreo aleatorio estratifcado, deberíamos de acceder a dicho listado (nuestro marco muestral), para así, dividir este en 2 estratos: benefciarios y no benefciarios. Luego, mediante la asignación de números de identifcación a cada unidad de los estratos, se procede, posteriormente, a la extracción aleatoria de integrantes de la muestra.

¿Cómo se extrae la muestra de nuestro marco muestral? Si queremos continuar con un muestreo aleatorio simple, siguiendo una tabla de números aleatorios o mediante un programa de computadora. Por otro lado, si optamos por un muestreo aleatorio sistemático, procederiamos a calcular el coefciente de elevación (N/n) y, mediante un procedimiento azaroso (usando una tabla de números, programa de computadora, etc.), se elige un número menor al coefciente de elevación y los restantes elementos de la muestra se obtienen sumando, sucesivamente, el coefciente de elevación, hasta completar, al menos, el tamaño de nuestra muestra.

De esta manera, se seleccionarán tanto una cantidad de individuos benefciarios como no benefciarios. ¿Cuántas unidades muestrales de nuestra muestra global asignar a cada estrato? Esto dependerá del proceso de afjación por el cual optemos. En este caso, si busco comparar benefciarios con no benefciarios en el impacto de la beca para reducir el abandono escolar y mejorar el compromiso con las tareas escolares, a mi me interesaria más tener un número igual de benefciarios y de no benefciarios para poder comparar estos de igual manera y no en función al peso proporcional de cada estrato. Por lo tanto, en la igual representación de los estratos en la muestra global, optaría por la afjación simple.

2- Responda si la siguiente proposición es VERDADERA o FALSA y justifique su respuesta

recuperando la bibliografía sobre el tema:

“Si tengo un R de Pearson de 0,60 entre clase social y calidad del empleo, puedo decir que la clase social explica el 36% de la calidad del empleo”.

Verdadero. El R de Pearson es una técnica que permite identifcar si existe una correlación lineal entre dos variables intervalares/razón, la intensidad de esta, y el sentido (positivo o negativo) de la curva. En el caso de que se presente una asociación entre dichas variables, podemos hablar de una correlación entre estas, es decir, un cambio sistemático entre las puntuaciones de las 2 variables.

Si estamos frente a la existencia de una correlación entre variables, podríamos hacer uso de una fórmula de una línea recta para obtener mejores estimaciones para valores de una variable independiente para cualquier valor dado de la variable dependiente. Al plasmar estos valores en los ejes, si forman una línea recta, podemos hablar de una recta de regresión que nos permita predecir valores en que van más allá de los datos de mis variables. El grado de fuerza de esta relación es medido por el R de pearson, y la elevación de este coefciente al cuadrado nos indica en qué porcentaje la variable independiente explica los valores de la variable dependiente. En el caso de tener un R de pearson de 0.60, al elevar este valor al cuadrado, nos da un 0.36. Esto me indicaria que la clase social me indica en un 36% la calidad del empleo.