Altillo.com > Exámenes > UBA - Farmacia y Bioquímica > Física
| Física | Trabajo Práctico: Electricidad | 2006 | Altillo.com |
ELECTRICIDAD
RESISTIVIDAD
OBJETIVO:
·
Comprobar la relación entre la resistencia, el material del cual está hecha la misma (resistividad), la longitud del conductor que la genera, y su sección.FUNDAMENTO:
Trabajo práctico basado en la relación existente entre la diferencia de potencial (voltaje) suministrada por una fuente y la resistencia que le opone el conductor al flujo de cargas. Esta relación se ve formulada en la siguiente ecuación:I = ΔV
R
En este TP se manipularan la resistividad (propiedad dependiente del material) de los conductores utilizados, así como su longitud y sección. La ecuación que rige esta relación es:
R = ρ
LA
MATERIALES:
·
Resistencias de Ni-Cr·
Resistencia de Hierro Galvánico·
Tablero·
TésterMÉTODO:
En primer lugar, prender el téster y colocarlo en la posición de resistencia de menor valor. Antes de realizar cualquier medición, verificar el error de cero que posea el instrumento de medición. Para ello, juntar las dos puntas del mismo y verificar que la lectura dé cero. En el caso de no ser así, hacer las correcciones en las sucesivas medidas.
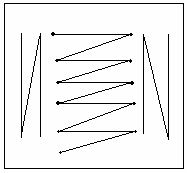
Los conductores en el panel estarán colocados como se muestra en el siguiente esquema. En el caso del conductor de Ni-Cr, colocar una las puntas del amperímetro en el primer tornillo que sostiene al conductor, e ir variado la segunda punta entre los demás tornillos. Determinar previamente la distancia que existe entre cada tornillo. Medir en cada caso la resistencia del conductor.
Además, en el caso del Ni-Cr de diámetro 0.346mm y del conductor de hierro galvánico, medir la resistencia que general entre sus extremos. Comparar los valores obtenidos.
En la siguiente figura, a la izquierda se encuentra el conductor de hierro galvánico, en el medio el de níquel cromo de diámetro 0,2 mm y a la derecha en de níquel cromo de diámetro 0,346 mm

Datos: Conductor Fe galvánico: D = 1mm
Largo total = 75 cm
Conductor Ni - Cr: D = 0.2mm
Distancia entre tornillos = 20 cm
Conductor Ni - Cr: D = 0.346mm
Largo total = 45 cm
RESULTADOS:
Conductor Fe galvánico:
R = 0,7 Ω
ρ = 0.000733
Conductor Ni - Cr : D = 0.346mm
R = 6,0 Ω
ρ = 253.8668 Ωxmm
Conductor Ni - Cr: D = 0.2mm
Tabla: Resistencia en función de la longitud
| Resistencia (Ω) | Longitud (cm) |
| 0,5 ± 0,1 | 0 |
| 8,0 ± 0,1 | 20 |
| 15,6 ± 0,1 | 40 |
| 23,1 ± 0,1 | 60 |
| 30,5 ± 0,1 | 80 |
| 38,2 ± 0,1 | 100 |
| 45,4 ± 0,1 | 120 |
| 52,8 ± 0,1 | 140 |
| 60,3 ± 0,1 | 160 |
| 67,9 ± 0,1 | 180 |
| 75,5 ± 0,1 | 200 |
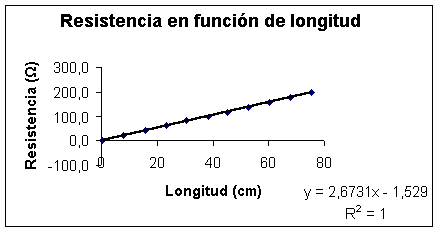
Gráfico: Resistencia en función de la longitud
ρ = 0.083978 Ωxmm
CONCLUSIÓN Y DISCUSIÓN:
En las experiencias se pudieron apreciar diferentes valores de resistencias y consecuentemente, las distintas resistividad de los materiales. En primer lugar, la resistividad que presenta el conductor de hierro galvánico es mucho menor a la que poseen cualquiera de los dos conductores de níquel-cromo. Esto se debe a que son de distintos materiales.
Por otro lado, se puede observar que entre los dos conductores de Ni-Cr, la resistencia es mayor cuanto menor es el diámetro. En este caso, el diámetro determina la sección del conductor mediante la ecuación: π x (d/2)2 donde la única variante es éste. En conclusión, entre mayor sea la sección menor será la resistencia del conductor. Además, la diferencia de diámetro también se ve reflejada en un cambio de resistividad. A mayor diámetro mayor resistividad.
Finalmente, se puede observar que la resistencia de un conductor depende de su longitud. Como se observa en el gráfico, al aumentar la longitud del conductor, aumenta la resistencia; ya que la resistividad y la sección son propiedades constante para un mismo conductor con sección similar en todo su recorrido.
Por todo ello, podemos concluir que la Resistencia depende directamente de la resistividad y de la longitud, pero inversamente de la sección que posee. Finalmente, pudimos corroborar la siguiente ecuación:
R = ρ
LA
POTENCIOMETRÍA
OBJETIVO
:·
Calcular la FEM (ε) y la resistencia interna de una fuente de poder.FUNDAMENTO:
Trabajo práctico basado en la diferencia de voltaje producida por una fuente real que posee resistencia interna.
Vab =
ε - ri x iEn el caso de que la fuente no posea resistencia interna (fuente ideal), el gráfico de voltaje en función de intensidad tiene pendiente nula y se rige por la ecuación:
Vab = ε
MATERIALES:
·
Resistencias·
Fuente de poder·
Cables conductores·
Amperímetro·
VoltímetroMÉTODO:
Mediante el juego de cables disponibles y las resistencias, armar distintos sistemas con resistencias unidas en paralelo, serie o una combinación entre ambas. Las suma de todas las resistencias se esquematiza en la siguiente figura como Req. Conectar el amperímetro en serie y voltímetro en paralelo. En cada caso, medir el
ΔV e i. Luego, graficar ΔV = f ( i ).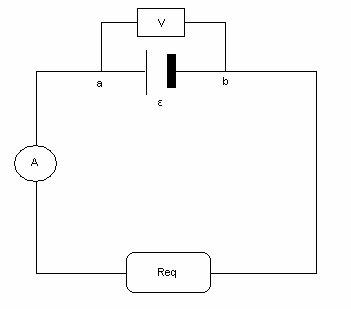
RESULTADOS
:
1) Una única resistencia: 2) Dos resistencias en serie:
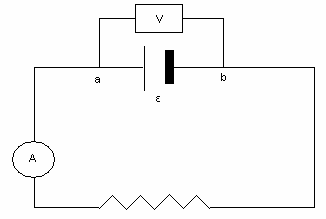

i = 55.4 mA i = 31.1 mA
V = 5.60 v V = 6.30 v
R = 101.08
Ω R = 101.29 Ω
3) Dos resistencias en serie y una en paralelo: 4) Tres resistencias en paralelo:


i = 74.5 mA i = 113.0 mA
V = 5.07 v V = 3.93 v
R = 102.07
Ω R = 104.34 Ω
5) Tres en serie: 6) Tres en serie y una en paralelo:


i = 22.2 mA i = 68.8 mA
V = 6.71 v V = 5.30 v
R = 100.75
Ω R = 102.71 Ω7) Dos en serie en paralelo con otras dos en serie: 8) Tres en serie en paralelo con dos más:


i = 55.7 mA i = 94.1 mA
V = 5.70 v V = 4.20 v
R = 102.33 Ω R = 104.14 Ω
Tabla: Voltaje en función de intensidad
| Intensidad (A) | Voltaje (V) |
| 0,0554 ± 0,0001 | 5,60 ± 0,01 |
| 0,0311± 0,0001 | 6,31 ± 0,01 |
| 0,0745 ± 0,0001 | 5,07 ± 0,01 |
| 0,1130 ± 0,0001 | 3,93 ± 0,01 |
| 0,0400 ± 0,0001 | 6,16 ± 0,01 |
| 0,0222 ± 0,0001 | 6,71 ± 0,01 |
| 0,0688 ± 0,0001 | 5,30 ± 0,01 |
| 0,0557 ± 0,0001 | 5,70 ± 0,01 |
| 0,0941 ± 0,0001 | 4,20 ± 0,01 |
Gráfico: Voltaje en función de intensidad

FEM = 7.382 v
ri = -31.467
CONCLUSIÓN Y DISCUSIÓN:
Mediante el gráfico, pudimos concluir que en nuestros s
istema la fuente de poder o FEM (ε) utilizada, posee una resistencia interna Esto se observa ya que el gráfico posee una pendiente distinta de cero. Es decir, está regida por la ecuación:Vab =
ε - ri . iEntonces, puede decirse que cuando aumenta la intensidad, el producto ri . i aumenta, por lo cual la Vab irá disminuyendo para que la FEM sea constante. Esto provoca un gráfico con pendiente negativa que representa la resistencia interna(ri) de la FEM. Además, al proyectar la recta en el eje de las ordenadas, se observa la fuerza electromotriz
(ε) de la pila, ya que se obtiene la diferencial de voltaje al pasar por la pila una intensidad nula. En nuestro caso, la ε = 7.382 v.CÁLCULOS:
Resistividad:
R = ρ
LA
Conductor de Fe gálvanico:
0,7Ω = ρ x (750mm/ {π x (1mm/2)
2})ρ = 0.000733
Conductor de Ni-Cr:
6,0Ω = ρ x (450mm/ {π x (0.346mm/2)
2})ρ = 253.8668 Ωxmm
Conductor de Ni-Cr:
R/L = 2,6731 =
ρ / {π x (0.2mm/2)2}ρ = 0.083978 Ωxmm
Potenciómetro:
Mediante la siguiente ecuación, calculamos las resistencia equivalente y sabiendo que todas las resistencias poseen igual valor, el de cada resistencia:
I =
ΔVReq
1) Una única resistencia:
Req =
5.60v / (55.4/1000)A = 101.08 Ωc/ R = 101.08 Ω
2) Dos resistencias en serie:
Req = 6.30v
/ (31.1/1000)A = 202.57 Ωc/ R = 101.29 Ω
3) Dos resistencias en serie y una en paralelo:
Req =
5.07v / (74.5/1000)A = 68.05 Ω1/Req = 1/2R + 1/R
c/ R = 102.07
Ω4) Tres resistencias en paralelo:
Req =
3.93v / (113.0/1000)A = 34.78Ω1/Req = 3/ R
c/ R = 104.34
Ω5) Tres en serie:
Req =
6.71v / (22.2/1000)A = 302.25Ωc/ R = 100.75
Ω6) Tres en serie y una en paralelo:
Req =
5.30v / (68.8/1000)A = 77.03Ω1/Req = 1/ 3R + 1/R
c/ R = 102.71
Ω7) Dos en serie en paralelo con otras dos en serie:
Req = 5.70v / (55.7/1000)A
= 102.33Ω1/Req = 1/ 2R + 1/2R
c/ R = 102.33 Ω
8) Tres en serie y dos en paralelo:
Req =
4.20v / (94.1/1000)A = 44.63Ω1/Req = 1/ 3R + 2/R
c/ R = 104.14 Ω