En la psicología es común el uso de Modelos teóricos para explicar las regularidades del comportamiento o el funcionamiento mental. Pero, en la estadística, los modelos teóricos que se usan describen el comportamiento de las variables (describen como se presentaría la variable de interés en la población que es objeto de estudio).
Modelo : es una construcción teórica, es una representación simplificada de la realidad que posibilita una mejor comprensión de la realidad , facilita su análisis e interpretación, formula conclusiones y realiza predicciones. Contar con un modelo para una variable le permite al investigador deducir conclusiones que luego confrontará con la realidad observada (las pondrá a prueba para ver si predicen bien lo que sucede en la realidad).
Para recordar : las frecuencias relativas nos informan que parte del todo corresponde a cada valor de la variable. Las frecuencias porcentuales representan lo mismo pero multiplicado por 100.
Probabilidades : las frecuencias relativas teóricas se van a llamar probabilidad para diferenciarlas de las frecuencias relativas muestrales. La probabilidad de un valor de la variable es la proporción de casos que se espera que ese valor de la variable tenga en una población. La probabilidad de un valor de la variable puede interpretarse como una medida de la posibilidad de que dicho valor sea observado.
Un valor de la variable imposible de ser observado en una población tendría una probabilidad igual a 0. Los valores de la variable posibles pero raros van a tener valores de probabilidad cercanos a cero. Los que son casi seguro de que se vayan a dar, tendrán valores de probabilidad cercanos a uno.
A veces se usan porcentajes para indicar probabilidades, pero, aunque la intención es la misma, estos valores no son probabilidades , sino que son porcentajes de posibilidades que expresan cuantas de cada 100 veces se espera que ocurra el suceso buscado
Se van a usar variables aleatorias. Se llaman así porque sus valores dependen del azar, tiene que ver con eventos cuyos resultados no podemos predecir con certeza, por ejemplo, cuando elegimos a un individuo al azar dentro de la población de alumnos de psicología, no sabemos si es hombre o mujer. Lo que es al azar es el procedimiento de elección de un individuo.
Un modelo teórico para una variable es una distribución de frecuencias relativas teóricas . Estas frecuencias relativas no están fundamentadas en la observación directa sino que son postuladas . Lo que justifica los valores que se proponen es la experiencia previa o a partir de ciertas condiciones teóricas.
Las frecuencias relativas en el modelo teórico se denominan probabilidades y es por esto que un modelo para una variable es una distribución de probabilidades.
La probabilidad de un valor de una variable tiene las mismas propiedades que las frecuencias relativas à es una cantidad no negativa y la suma de las probabilidades asignadas a los valores de la variable es uno.
Se pueden calcular las medidas de tendencia central y la variabilidad: (como antes se hacía en estadística descriptiva, es decir, la muestra)
La media se obtiene sumando los productos de los valores de la variable y multiplicandolas por sus correspondientes probabilidades y se simboliza con la letra griega "μ". Así, la diferenciamos de la media muestral simbolizada con X̅
°° "x" seria la variable como 1, 2, 3, 4 y "p" es la probabilidad de que se de esa variable
--> μ = x. p + x . p + x . p...
(μ es igual a sumar los resultados que te da hacer la cuenta "x . p" para cada variable y su probabilidad)
- La varianza se obtiene sumando los cuadrados de los desvíos a la media por la probabilidad correspondiente y se simboliza con la letra griega " σ2 "
°° "x" seria la variable como 1, 2, 3, 4; "p" seria la probabilidad y "μ" seria la media, pero de la población
à σ² = (x - μ) ² . p + (x - μ) ² . p... (σ2 sería igual a sumar los resultados que te da hacer la
cuenta de "(x - μ)² . p" para cada variable y su probabilidad, μ no cambia, solo cambian las "x" y las "p")
- El desvío es la raíz cuadrada de la varianza y es por eso que se representa con el "σ"
(Estos resúmenes estadísticos se representan con letras griegas ya que se tratan de parámetros porque son propiedades descriptivas de la población)
Si la realidad que conocemos a través de las muestras coincide con lo planteado en el modelo de distribución de probabilidades, se puede decir que el modelo se sostiene.
La estadística desarrolló una gran variedad de modelos de probabilidades que describen el comportamiento de distintos tipos de variable. Cada modelo tiene su nombre como el "Modelo Binomial", para variables cuantitativas discretas, y el "Modelo Normal", para variables cuantitativas continuas.
Modelo Binomial
Una variable cuantitativa discreta sigue un modelo de probabilidad binomial.
Este modelo cuenta la cantidad de éxitos que ocurren en "n" observaciones de una variable dicotómica que tiene un parámetro "p", que son independientes y con la misma probabilidad de éxito "p".
Ej: se tira 4 veces un dado y se registra el número de veces que sale el 2 en las 4 veces que lo tire. El resultado que se obtiene en cada lanzamiento se puede considerar una variable dicotómica con probabilidad de éxito de 1 sobre 6 ya que un dado tiene 6 caras y por lo tanto en las 4 veces que se tira el dado pueden salir 6 números distintos.
à La variable es la "cantidad de 2 en cuatro tiradas del dado" y es una variable binomial. Sus parámetros son: "n" = 4 y "p" = 1/6 (es decir que las observaciones o "n" observaciones son las veces que tiro el dado, las veces que puedo observar si sale o no esa variable. La "p" o las probabilidades son 1 de 6 ya que hay una posibilidad de que salga el 2 en cada tirada de dado).
Los valores de una variable binomial son 0, 1, 2, 3, 4, ..., n.
Las probabilidades asociadas a cada uno de los valores de la variable Binomial resultan del uso de una formula matemática que involucra a "n" y a "p".
Condiciones necesarias para poder aplicar el Modelo Binomial
1) condición de estabilidad: dice que la probabilidad de éxito (la probabilidad de obtener el valor de la variable dicotómica que estamos buscando) debe permanecer constante en las "n" observaciones de la variable dicotómica.
En el ej anterior, la probabilidad de que salga 2 cuando tiro los dados siempre es 1 de 6, no cambia por cada vez que tiro los dados, sino que se mantiene estable o constante.
Supongamos que tenemos un bolillero que contiene 50 bolitas negra y 50 bolitas blancas, la probabilidad de obtener una bolilla blanca es de 0,5. Pero si al momento de obtenerla, la saco del bolillero entonces la probabilidad va a cambiar y por lo tanto perdería la condición de estabilidad y no podríamos aplicar el modelo binomial.
2) condición de independencia: refiere a que la probabilidad de tener éxito en una observación no aumenta ni disminuye si se conoce el resultado de otra observación. En el ej anterior, la probabilidad de que salga 2 en la tercera tirada no cambia aunque sepa que en las anteriores tiradas salió 2. Conocer los resultados de observaciones previas, no modifican mi probabilidad de predecir los ensayos que van a venir.
Modelo de Distribución Normal
Recordemos que cuando se habla de modelo de distribución, se habla de la forma que adquieren los datos debido a su variabilidad. Dependiendo de cómo es esa forma, se pueden derivar probabilidades teóricas de ocurrencia de un evento.
Se pueden tener distintos patrones según la forma que tomen, una de las formas o patrones es la de distribución normal
En este modelo, "μ" y "σ" son sus parámetros (propiedades descriptivas de las poblaciones, media poblacional y desvío poblacional)
°° "N" significa que es una distribución normal
--> N (μ y σ) = esta combinación de parámetros o de datos nos va a dar una distribución normal
Variables que se ajustan a este modelo: inteligencia, tiempo de reacción, aptitudes, rendimiento escolar
Características del modelo
- es un modelo para variables cuantitativas continuas
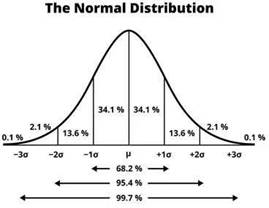
- hablar de la "Curva Normal", o sea de la curva de este modelo, es lo mismo que hablar de la "Campana de Gauss" ya que son iguales, se distribuyen igual . Recordemos que la "Campana de Gauss" representa que los valores de mayor frecuencia son los valores que están en el medio (la gran mayoría de las personas obtienen valores intermedios y es poco probable que haya gente que obtenga valores que vayan más a los extremos)
- casi un 70% de las personas va a estar en los valores más frecuentes, luego se va a ir aumentando con forme pasen los desvíos. Es decir, entre el -σ y σ (con μ en el medio incluido) va a estar casi el 70% de las personas, entre el -2σ y 2σ va a estar el 95% de
las personas y entre el -3σ y 3σ va a estar el 99% de las personas
 |
Propiedades de la Distribución Normal
- es simétrica con respecto a un valor central (μ) donde coinciden las tres medidas de
tendencia central (media, moda y mediana).
- es asintótica con respecto al eje de las abscisas, es decir que la curva no toca el eje de las X salvo en ± infinito.
- hay una familia de curvas normales y la más importante es aquella conmedia 0 y desviación típica 1 à distribución normal unitaria
- los puntos de inflexión se encuentran en los puntos correspondientes a la media ± una desviación típica (μ ± σ). Están en donde esta más o menos el 70% de las personas.
- cualquier combinación lineal de variables aleatorias normales se ajusta también al modelo normal
Dos interrogantes:
¿Cuál es la probabilidad acumulada (es decir, el area) asociada a un determinado valor de la variable?
¿Qué valor de la distribución se asocia a una probabilidad asociada dada?
Valor y distribución normal unitaria, hablamos de puntuaciones típicas
Z = x – μ
σ
Antes de pensar las resoluciones de un problema de distribución normal hay que :
1) identificar claramente los parámetros (es decir μ y "σ"
2) tener en claro cuál es la información que necesito obtener (área o puntaje)
Es puntaje/valor/centil? o es área/porcentaje/rango percentilar? Hay dos ejes verticales.
3) definir si corresponde tipificar o destipificar
Tipificar à Z = x – μ
σ
Destipificar à X = Z . σ + μ
4) no olvidar que no es lo mismo la puntuación Z que el valor de la puntuación original
Distribución de la media muestral
Para recordar:
a- El principal objetivo de la estadística inferencial es establecer conclusiones relativas a los parámetros poblacionales a partir de los estadísticos muestrales. Para eso es necesario conocer la relación entre ambos, o sea, establecer una relación entre las características poblacionales y las características muestrales.
b- Un parámetro es una propiedad descriptiva de una población, es una característica fija, generalmente numérica, de la población de observaciones de los valores de una variable y se simbolizan en letras griegas. Por ejemplo: puntaje medio (μ) en el test de autoestima de todos los alumnos de 7mo grado de CABA. Varianza poblacional (σ al cuadrado) de los puntajes en una prueba de memoria de todos los ingresantes al CBC. Proporción (Pi, la letra de matemática) de promocionados en la población de alumnos de estadística del cuatrimestre pasado.
c- Un estadístico es una propiedad que describe a una muestra, es una característica muestral que se calcula en función de las observaciones muestrales. Por eso su valor va a depender de los valores de la variable que tomen los individuos seleccionados para ser parte de la muestra. Por ejemplo: puntaje medio (equis raya) en el test de autoestima de 50 alumnos seleccionados al azar de 7mo grado de CABA. Varianza (s al cuadrado) de los puntajes en una prueba de memoria de una muestra aleatoria de 80 ingresantes del CBC. Proporción (p) de promocionados en una muestra de 40 alumnos de estadística tomados al azar del cuatrimestre pasado
Como el valor del estadístico varia según la muestra, entonces se lo puede considerar como una viable porque sus valores dependen de la muestra que sea seleccionada.
La media, varianza y proporción muestral son estadísticos ya que se calculan sobre la base de observaciones de la muestra. Cada muestra de valores de una variable X brinda un valor medio, una varianza y una proporción de ocurrencia de algún suceso de interés determinado para esa muestra.Si se cambia la muestra, cambian los valores de los estadísticos mencionados.
¿Qué relación existe entre un parámetro μ y el estadístico X̅? (cuando la variable x es normal)
Es razonable esperar una distribución para la media muestral donde es más probable encontrar las medias muestrales en torno a la media poblacional . A medida que los valores de medias muestrales se alejan hacia cualquiera de los dos extremos es menos probable que se den, es decir, es menos probable encontrar muestras que tengan esas medidas .
La media muestral es una variable y al igual que cualquier otra variable tiene su propia distribución de probabilidad. Si podemos establecer cuál es esa distribución, entonces podemos calcular probabilidades asociadas a los posibles valores estadístico.
La distribución muestral de un estadístico es la distribución que empareja posibles valores de un estadístico con las probabilidades de verificación.
La desviación típica de la distribución muestral de un estadístico recibe el nombre de error típico.
La distribución de la media muestral es una distribución teórica que asigna una probabilidad (o una densidad de probabilidad) concreta a cada uno de los valores que puede tomar la media muestral en todas las muestras del mismo tamaño que es posible extraer de una determinada población . Proporciona todos los valores que puede tomar X ̅ para muestras de tamaño "n", junto con la probabilidad de obtener cada valor si el muestreo es aleatorio a partir de la población.
à Variable: X̅ (media muestral) de muestras aleatorias de tamaño "n". La media muestral se comporta como una variable dado que al cambiar de muestra cambian las medias.
àPoblación de individuos: todas las muestras aleatorias de igual tamaño (n) posibles de ser seleccionadas de la población de individuos de la variable X. Es la población sobre las cual se observa la variable media muestral
à Población de observaciones: todas las X̅ posibles de ser obtenidas si seleccionamos muestras aleatorias de tamaño "n" de la población.
à Como toda distribución, tiene una media y un desvío estándar:
- μ de X̅ = media poblacional de la variable X̅ (es una media poblacional porque es una media de todas las medias muestrales posibles, saca la media de todas las medias muestrales de tamaño "n" posibles de ser seleccionadas en una población determinada).
- σ de X̅ =desviación estándar poblacional de la variable X ̅ = error típico de la media (es una desviación estándar poblacional porque sacas el desvío de todas las medias muestrales posibles de tamaño "n" posibles de ser seleccionadas en una población determinada). La variabilidad de entre las medias muestrales, se da por los errores de estimación y es por eso que se le dice error típico o error estándar de la media.
à El centro de la distribución muestral de X̅ es el mismo que el de la distribución poblacional de la variable X à μ de X̅ = μx
à La variabilidad de la distribución muestral de X ̅ es menor a la de la variable X. ¿Cuánto menor? Depende del tamaño de la muestra:
- Cuanto más grande sea el "n" (tamaño) de la muestra, más se parecerá la X̅ a la poblacional y por lo tanto la variabilidad o dispersión de las X̅ con respecto a la media poblacional será menor y las medias muestrales varían menos.
- Por lo tanto, la varianza de la distribución muestral de X̅ es = a la varianza poblacional de X dividida por el tamaño de la muestra
2 2
σ --- = σ --- /n
X̅ X̅
- La desviación típica de la distribución de la media muestral es = a la desviación típica poblacional de X dividida por la raíz cuadrada del tamaño de la muestra
σ de X = σ de X̅
√n
¿Qué variable tiene mayor variabilidad? ¿La variable X o la variable X̅?
Son dos variables distintas, sin embargo, la variable X tiene mayor variabilidad que la variable X ̅ porque el hecho de promediar los valores muestrales tiene el efecto de homogeneizarlos. Por ej: poder elegir al azar alumnos de la población y encontrar alguno con nota 2 o 9 pero es casi imposible encontrar en una muestra a alguien de la población que tenga por media la nota 2.
El conjunto de todos los valores de X se agrupo en subconjuntos de tamaño "n" = 40 por lo que cada muestra tiene a 40 valores que perdieron su identidad para ser representados por la media muestral. Esto tiene efecto de disminuir las diferencias entre las distintas medias muestrales respecto de las diferencias entre los X sin agrupar
Si la variable X tiene distribución normal con parámetros μx y σx , entonces la distribución muestral de la variable X̅ es también normal con parámetros μ de X̅ = μx y σ de X̅ = σ de X̅ / √n. Esto se representa:
X~N (μx; σx) o X̅~N (μ de X̅; σ de X̅ / √n)
(X o X̅ se distribuye, ~, normalmente, "N" con...)

|
Si X̅ es una variable aleatoria que tiene distribución normal, entonces la transformación de la variable X ̅ en puntuaciones Z se distribuye normalmente con media = 0 y desviación típica = 1 .
Z = X̅ - μ de x ~ N (0 ;1)
σ /√n
Entonces, se puede usar la transformación Z y la distribución normal tipificada para conocer las probabilidades asociadas a cada uno de los diferentes valores del estadístico X̅ en su distribución muestral
Propiedades :
- Si la variable X tiene distribución normal con media μ y desvío estándar σ, la variable X̅ tiene distribución normal con media μ y desvío de σ / √n
- La media muestral estandarizada sigue la distribución normal unitaria con media = 0 y desviación = 1. Las probabilidades para distintos valores de X ̅ se pueden obtener transformando estos valores a puntuaciones X buscando la probabilidad correspondiente en la distribución unitaria
à Z = X̅ - μ de x ~ N (0 ;1)
σ /√n
- La media muestral estandarizada cuando σ es desconocido se obtiene mediante la
transformación :
t = X̅ - μ de x ~ tn-1
S / √n
Esta transformación no se distribuye normalmente, sino según el modelo de probabilidad “t de student” con n-1 grados de libertad.
- Cuando la variable X no es normal, la distribución de la variable X ̅ resulta aproximadamente normal cuando los tamaños muestrales son grandes, o sea n > 30 (teorema central del límite).
Es habitual que en una investigación se pretenda determinar la veracidad de una afirmación en la población de referencia.
Como no se puede acceder a la información de todos los individuos de la población en cuestión, lo que se hace es evaluar la veracidad de estas afirmaciones en la muestra disponible para determinar si las conclusiones obtenidas son válidas para la población de pertenencia.
Para que esto sea así, la muestra debe ser representativa de la población y deberán aplicarse métodos de inferencia estadística para decidir sobre la veracidad de la afirmación, porque estos permiten calcular el nivel de error de esa decisión.
Este método del que estamos hablando es el contraste de hipótesis que es un instrumento estadístico que permite evaluar a partir de los datos de una muestra representativa, la veracidad de afirmaciones hechas sobre una población . Puede ser entendido como un método de toma de decisiones y se lo conoce también como prueba estadística y como prueba de significación.
En el contraste de hipótesisse evalúa la veracidad de una hipótesis que se va a llamar hipótesis científica que es una afirmación referida a una o varias características de una población. Pero esta no es directamente evaluable a partir de los datos muestrales y por lo tanto es necesaria transformarla en una hipótesis estadística que tiene que ser completamente equivalente a la original pero plasmada y representada de forma que se pueda analizar los datos muestrales mediante un método de inferencia estadística o mediante métodos estadísticos.
Entonces, la teoría de contraste de hipótesis hace referencia a dos hipótesis :
à Hipótesis nula (H0)
à Hipótesis alternativa (H1 o complementaria de la anterior)
Siempre la decisión tomada es sobre la H 0 , es decir que cuando los datos de la muestra nos hagan decidir que H0 no es verdadero, vamos a hablar de rechazar H0. Y cuando los datos nos hagan decidir que H0 es verdadero, entonces la vamos a aceptarla o no rechazarla.
Existen dos posibles errores que pueden cometerse cuando se utiliza esta metodología : (no tiene que ver con cuan representativa es la muestra, sino con el hecho de elegir si es verdadera o no:
- error de tipo 1 : rechazar la hipótesis nula cuando es verdadera. En términos probabilísticos, lo llamamos probabilidad de error de tipo 1 al nivel de significación del test o α que se fija en 0.05 o 0.01.
- error de tipo 2: aceptar la hipótesis nula cuando es falsa. En términos probabilísticos, lo llamamos probabilidad de error de tipo 2 al β que va a depender del tamaño de la muestra considerada.
Para poder definir el contraste de hipótesis que puedan controlar estos errores es necesario pasarlos a una serie de supuestos la mayoría de ellos probabilísticos. Estos son un conjunto de afirmaciones que se toman como válidas y que hacen referencia a la distribución de las variables del problema y a otras cuestiones vinculadas. Estos supuestos conforman las condiciones teóricas necesarias para el desarrollo de los contrastes de hipótesis.
à Los supuestos deben tener una muestra representativa aleatoria
Basado en la variable (necesario medir para resolver el contraste la hipótesis) y en los supuestos que se formularon, siempre es posible definir en un contraste de hipótesis un estadístico de prueba o estadístico de contraste. Este es un indicador numérico calculado a partir de la información de la muestra cuya distribución es conocida, permite decidir sobre la veracidad de las hipótesis .
Los contrastes de hipótesis tienen definidos una regla de decisión. Este es el criterio que fija el contraste de hipótesis para rechazar o no H0. Puede basarse o fijarse de dos formas:
à Definiendo la zona de rechazo del contraste de hipótesis
à Calculando la probabilidad de rechazar H0 cuando es verdadera, dado el valor del estadístico obtenido en la muestra. Valor - p o P - value (valor = probabilidad).
Consiste en la comparación de esta probabilidad con el nivel alfa que el investigador haya fijado previamente. Entonces si el valor de "p" y la probabilidad (que llamamos "valor") es menor que alfa, entonces se rechaza la hipótesis. Pero si el valore de "p" es mayor que alfa, no se rechaza la hipótesis nula
Contraste de hipótesis para la media de una distribución normal con sigma conocido
Este contraste de Hipótesis es habitual cuando es necesario verificar Hipótesis que pueden representarse a partir de la media de una variable. Para realizar esta técnica, se va a basar en el supuesto de normalidad de la variable, o sea que supondremos que la variable X del problema sigue una distribución normal con media μ y desvío σ en la población, y que la Hipótesis científica del investigador puede ser expresada como una Hipótesis estadística usando μ.
La muestra aleatoria es como un conjunto de variables normales. Sea x1, ..., xn son una muestra aleatoria de una variable X:
Si X tiene una distribución N (μ; σ), entonces todas las xi (muestras) ~ N (μ, σ)
à el estimador óptico (estimador con menos varianza) de μ es el promedio, es decir: el promedio de μ = X̅
à el estimador óptico (estimador con menos varianza) de σ es el desvío standard, es decir que:
El promedio de σ = S = | Σ (xi - X̅)2
√ n - 1
àSi X tiene distribución N (μ; σ), entonces la distribución del promedio es:
X̅ ~ N (μ; σ/ √n)
à Al tipificar X̅ se obtiene una distribución normal unitaria
![]() Tipificación de X
̅
= X̅ - μ ~ N (0, 1)
Tipificación de X
̅
= X̅ - μ ~ N (0, 1)
σ/ √n
El contraste de una Hipótesis para la media de una distribución normal con sigma conocido tiene los siguientes elementos
àLas hipótesis a contrastar que pueden ser de tres tipos diferentes:
- contraste bilateral HA ≠ μ0
- contraste unilateral derecho HA tiene al μ > μ 0
- contraste unilateral izquierdo HA tiene al μ < μ 0
à Los supuestos en los que se basa:
- se cuenta con una muestra aleatoria de tamaño "n"
- la distribución de la variable del problema seguiría la distribución normal de la población.
- el desvío standar poblacional, el desvío standar de esa variable, es conocido
à El estadístico de prueba es:
E = X̅ - μ 0 (es decir la tipificación de X̅)
σ/ √n
Y su distribución es E ~ N (0, 1) bajo la Hipótesis nula
à Según el contraste elegido, la región de rechazo o zona critica será:
°° E = estadístico
- contraste bilateral:
E ≤ - Z α /2 o E > Z α /2
- contraste unilateral derecho E > Z α
- contraste unilateral izquierdo
E ≤ -Z α
à Regla de decisión: se rechaza la hipótesis nula si el estadístico de prueba cae dentro de la zona de rechazo
à Regla de decisión basada en el Valor-p: forma más sencilla de decidir usando un contraste de Hipótesis que es usando el valor-p. El valor-p es la probabilidad de rechazar H0 de acuerdo con el valor obtenido con el estadístico.
- si el valor-p es menor o igual que α se rechaza la Hipótesis nula
- si el valor-p es mayor que alfa no se rechaza la Hipótesis nula
Contraste de hipótesis para la media de una distribución normal con sigma desconocido
Lo habitual es que μ no sea conocido y por lo tanto σ menos.
Este contraste de hipótesis sirve para tomar decisiones acerca del verdadero valor poblacional que corresponde a la media de una variable normal cuando no se conoce σ .
Supondremos que la variable X del problema sigue una distribución normal con media = μ y desvío = σ en la población, ambos desconocidos, y quela hipótesis científica del investigador puede ser expresada como una hipótesis estadística usando μ.
El contraste de una Hipótesis para la media de una distribución normal con σ desconocido, tiene los siguientes elementos
à Independientemente de que σ sea desconocido o conocido, cuando las Hipótesis a contrastar pueden expresarse en términos de la media y una normal, las Hipótesis a contrastar y los supuestos son los mismos:
- contraste bilateral HA ≠ μ0
- contraste unilateral derecho HA tiene al μ > μ0
- contraste unilateral izquierdo HA tiene al μ < μ0
à Supuestos en los que se basa
- se cuenta con una muestra aleatoria de tamaño "n"
- la distribución de la variable del problema seguiría la distribución normal de la población.
à Estadístico de prueba
- E = X̅ - μ 0
S/ √n
à Su distribución es E ~ tn-1 bajo H0
à Zona critica
- contraste bilateral
E ≤ - t a/2 o E > t a/2
- contraste unilateral derecho E > t a
- contraste unilateral izquierdo
- E ≤ -t a
à Regla de decisión
- Se rechaza la Hipótesis nula si el valor del estadístico cae dentro de la region de rechazo
à Regla de decisión basada en el Valor-p: forma más sencilla de decidir usando un contraste de Hipótesis que es usando el valor-p. El valor-p es la probabilidad de rechazar H0 de acuerdo al valor obtenido con el estadístico.
- si el valor-p es menor o igual que alfa se rechaza la Hipótesis nula
- si el valor-p es mayor que alfa no se rechaza la Hipótesis nula
La diferencia en comparación con el contraste anterior donde σ era conocido tiene que ver con lo siguiente:
Cuando conozco sigma, el denominador que forma el estadístico de prueba incluye a sigma en la cuenta. Pero cuando sigma no es conocido, hay una imposibilidad para calcular al estadístico de prueba y la solución que sea da es reemplazar a sigma con su derivador original que es el desvío estándar, el que proviene de la muestra "S". Como consecuencia, el estadístico pasa de tener una distribución normal con parámetro (0; 1) a la distribución “t de student”. Esta distribución está centrada en 0 y es muy similar a la normal pero no igual. Tiene un solo parámetro llamado "grados de libertad" o "n-1" (el tamaño muestral menos 1).
Contraste de hipótesis para comparación de medias poblacionales
Es una técnica frecuentemente usada para evaluar el comportamiento de una variable en dos poblaciones distintas.
Es adecuada para comparar dos poblaciones de individuos en alguna variable de interés.
Es ideal para evaluar la eficacia de un tratamiento y se puede hacer de dos formas diferente, o sea, usando dos tipos de contrastes distintos:
- con un contraste de Hipótesis para medias de poblaciones independientes : un grupo de sujetos se les aplica un tratamiento y al otro no y se los compara en alguna variable de interés.
- con un contraste de Hipótesis para medias de poblaciones relacionadas (muestras apareadas): un grupo de sujetos se los mide en una variable de interés antes y después de aplicarles un tratamiento y se comparan los puntajes obtenidos
Contraste de Hipótesis para medias de poblaciones independientes
Hay una variable de interés que se mide en las dos poblaciones que se quieren comparar . Además, esta variable de interés, se supone que sigue una distribución normal en cada una de las poblaciones donde los parámetros poblacionales son distintos entre ambas poblaciones , es decir que no son similares, el tamaño de dicha muestra puede variar, por ejemplo.
Los contrastes de Hipótesis para la comparación de medias se hacen mediante la resta de ellas:
- La hipótesis nula presenta μ1 - μ2 = d0
- Las hipótesis alternativas pueden ser:
Ha: μ1 - μ2 ≠ d0 Ha: μ1 - μ2 > d0 Ha: μ1 - μ2 < d0
E = | X̅1 - X̅2 - d0 ~ N (0, 1)
| σ1 ^2 + σ2^2
√ n n
Cuando los desvíos poblacionales (σ) son desconocidos, el estadístico de prueba es:
E = | X̅1 - X̅2 - d0 ~ tm+m -2
| Sp . (1 1)
√ (n m)
Regla de decisión : se rechaza la Hipótesis nula si el valor del estadístico cae dentro de la regio de rechazo
Regla de decisión basada en el Valor-p: forma más sencilla de decidir usando un contraste de Hipótesis que es usando el valor-p. El valor-p es la probabilidad de rechazar H0 de acuerdo al valor obtenido con el estadístico.
- si el valor-p es menor o igual que alfa se rechaza la Hipótesis nula
- si el valor-p es mayor que alfa no se rechaza la Hipótesis nula
Contraste de Hipótesis para medias de poblaciones relacionadas (muestras apareadas)
En este caso, la muestra de individuos es única, es esta la que provee las mediciones de la variable antes y después de la aplicación del tratamiento en cuestión. Cada valor de tratamiento esta vinculado con un valor post tratamiento ya que esas mediciones son tomadas siempre sobre los mismos individuos . Ambas muestras se suponen que provienen de una distribución normal pero eventualmente los parámetros de estas pueden ser diferentes .
El tipo de Hipótesis que pueden contrastarse en este tipo de problemas es similar al anterior ya que quedan expresados en términos de las medias de ambas poblaciones:
- H0: μD = d0
- HA: μD ≠ d0
- HA: μD > d0
- HA: μD < d0
El estadístico de prueba es:
E = X̅1 - X̅2 - d0 ~ tn-1
Sd/ √n
Coeficiente de correlación R de Pearson
Descubrir la relación entre variables constituye uno de los objetivos de la psicología, y la estadística desarrollo instrumentos para la tarea de detectar y cuantificar esta relación entre series de observaciones. Por ejemplo, un grupo de investigadores desea explorar si la cantidad de acciones solidarias en una muestra de adultos se asocia con un mayor nivel de felicidad.
El coeficiente de correlación de Pearson (representado por la "r") es un índice que mide la relación lineal entre dos variables cuantitativas . Puede valer entre -1 y 1, no tiene dimensión.
Es importante destacar que el "r"informa sobre si las variables se asocian linealmente, pero esa asociación no supone una causalidad
¿Como se interpretan los coeficientes r de Pearson?
Hay que separar dos aspectos distintos:
- cuantía: se refiere al grado en que la relación entre dos variables queda bien descrita con un índice de asociación lineal como r.
Un valor de más/ menos 1 indica un grado perfecto de asociación entre las dos variables, en la medida en que el coeficiente de correlación se acerca a 0 la relación entre las dos variables será más débil.
- sentido: se refiere al tipo de relación (directa, de 0 a 1, o inversa, de 0 a -1).
La dirección de la relación la indica el signo del coeficiente, un signo + indica una relación directa o positiva, y un signo - indica una relación inversa o negativa entre dos variables.
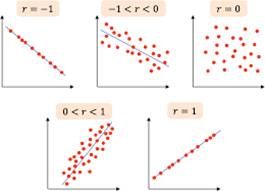
Sus gráficos se llaman diagramas de dispersión o dispersogramas y la configuración de puntos resultante se denomina nube de puntos.
Relación lineal directa o positiva
Se detecta entre dos variables cuando covarian en el mismo sentido . Es decir, cuando a valores bajos de una de ella corresponden valores bajos de la otra, a valores medios de una le corresponden los valores medios de la otra y a valores altos de una le corresponden los valores altos de la otra.
Relación lineal inversa o negativa
Se detecta esta entre dos variables cuando covarian en sentido contrario, es decir, cuando a valores bajos de una de ellas, corresponden valores altos de la otra
Relación lineal nula
Un r de aproximadamente 0 puede deberse a dos grandes casos:
1) las dos variables son independientes, de manera que no están asociadas linealmente de ninguna forma
2) las dos variables están relacionadas, pero no de manera lineal de manera que el r de Pearson no capta esa relación
|
>=10.zi+50
b) Escala de CI (cociente intelectual) : que tiene una media = 100 y una desviación típica = 15
---> CIi = 15.zi + 100