Altillo.com > Exámenes > UBA - CBC > Álgebra
|
Álgebra |
1° Parcial |
2° Cuat. de 2005 | Altillo.com |
1) Sea Π1 el plano de ecuación
3x + 2y - 6z = 1 y sea Π2 el
plano que pasa por (1,-1,0) , (0,-2,-1) y (3,-1,0). Hallar una recta L
tal que: ![]() ø
,
ø
, ![]() ø
y (2,2,1)
ø
y (2,2,1) ![]() L.
L.
2) Sean 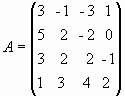 y
y  .
.
Hallar todos los valores de A![]() R
para los cuales el sistema Ax=x+b, con x
R
para los cuales el sistema Ax=x+b, con x![]() R4x1,
es compatible. Para algunos valores de a hallados, resolver el sistema.
R4x1,
es compatible. Para algunos valores de a hallados, resolver el sistema.
3) Sean S = {x![]() R4
/ 2x1 + 3x2 - x3 + 3x4 = 0}y
T = {x
R4
/ 2x1 + 3x2 - x3 + 3x4 = 0}y
T = {x![]() R4
/ -x1 + x2 +x4 = x1 - 3x3 = 0}.
Hallar una base de R4 que contenga a una base de S y a una base de T. Encontrar
las coordenadas del vector (2,1,1,0) en dicha base.
R4
/ -x1 + x2 +x4 = x1 - 3x3 = 0}.
Hallar una base de R4 que contenga a una base de S y a una base de T. Encontrar
las coordenadas del vector (2,1,1,0) en dicha base.
4) Sean S = <(1,0,-1,0) , (1,0,0,1) , (0,1,1,0)> y T = {x![]() R4
/ x1 - x3 + x4 = 0}
R4
/ x1 - x3 + x4 = 0}
Hallar, si es posible, subespacios W1, W2 y W3 tales que: W1![]() W2 = S
; W1
W2 = S
; W1![]() W3 =
T y W1
W3 =
T y W1![]() W2
W2
![]() {0}
{0}