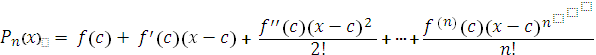
Este polinomio Pn tiene la particularidad que las derivadas en c coinciden
con las derivadas en c de la función f, es decir:
=
,
=
,
=
, ...,
=
Resto de Taylor
APLICACIÓN
- Aproximación de un valor y del error cometido -
1- Definir
2- Armar el polinomio centrado en el número más cercano al que se quiere calcular cuyo resultado en la función sea exacto, y la fórmula del resto
3- Reemplazar en el polinomio el valor que se quiere aproximar(x)
4- Reemplazar el mismo valor en la fórmula del resto
5- Acotar el módulo del error en el valor más grande(
)
- Calcular el grado del polinomio para que sea menor a cierto error -
1- Calcular la fórmula general del resto (
)
2- Evaluarlo en el valor donde se quiere calcular(x)}
3- Acotar el módulo al error máximo que se quiere cometer(
)
4- Despejar n y probar valores que satisfagan la ecuación
Se llama integral indefinida de una función a sus infinitas primitivas.
Una primitiva de una función
continua es una función
si se verifica que la derivada de
es
.
Si
entonces
Propiedades
a)
b)
Metodos de integracion
Cada regla de derivación tiene una correspondiente regla de integración.
➤ (Regla de la cadena) →Sustitución :
-
➤ (Regla del producto) →Por partes :
-
➤ Fracciones simples:
- si
y
son funciones polinomiales y el grado de
(si el grado de
primero hay que dividir
entre
):
- CASO I(
es un producto de factores lineales distintos):
donde
son las raíces del denominador
- CASO II(
es un producto de factores lineales, de los que algunos se repiten):
Teorema Fundamental del Calculo
➔ Parte 1:
- si
entonces
∴
- propiedad → si
entonces
➔ Parte 2:
-
donde
es una primitiva de
Calculo de area
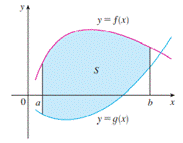
El área A de la región limitada por las curvas
y las rectas
es:
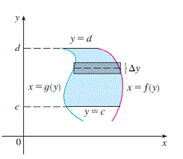
Algunas regiones se manejan mejor si se consideran a x como una función de
y. El área entre las curvas
y las rectas
y
es:
Ecuaciones diferenciales
- Son ecuaciones en las que la incógnita es una función y contienen su derivada
- La solución general de una ecuación diferencial es una familia de
ecuaciones que difieren en la constante. La solución particular cumple con
alguna condición adicional (ej:pasar por un punto
)
, entonces
Sucesiones
- Es una función con dominio en los naturales
donde
son los términos
- Si
(existe), la sucesión converge. De lo contrario diverge
- Una sucesión está acotada por arriba si
, y acotada por abajo si
.
- Toda sucesión monótona y acotada es convergente
- Es una sucesión formada por la sumatoria de otra sucesión
- Si la sucesión {
} es convergente y
entonces
∴ es convergente y el número
se llama suma de la serie
- Si
es convergente entonces
. Por lo tanto, si
o
la serie diverge.
• Serie geométrica ➜
es una caso especial de las series de potencia(
)
- si
converge y su suma es
- si
diverge
• Series p ➜
- si
converge
- si
diverge
Criterios para determinar la convergencia
➤ Comparación
- Si
es convergente y
entonces
es convergente
- Si
es divergente y
entonces
es divergente
➤ Leibniz (serie alternada) ➜
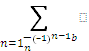
- Si cumple con
i)
ii)
entonces la serie es convergente
- si
converge
es absolutamente convergente
➤ D’alambert (prueba de la razón)
- Si
, entonces la serie
es convergente absoluta
- Si
,
diverge
- Si
, no es concluyente
➤ Cauchy (prueba de la raíz)
- Si
,
converge
- Si
, la serie diverge
- Si
, no es concluyente
Intervalo y radio de convergencia
- El intervalo de convergencia consiste en todos los valores de x para los que una serie converge. Para conocerlo:
i) Usar criterios (Cauchy/D’alambert)
ii) Aplicar condición de convergencia (
)
iii) Evaluar los bordes del intervalo
- El radio de convergencia es la mitad de la longitud del intervalo