Altillo.com > Exámenes > San Andrés > Matemática I

Problema 1:

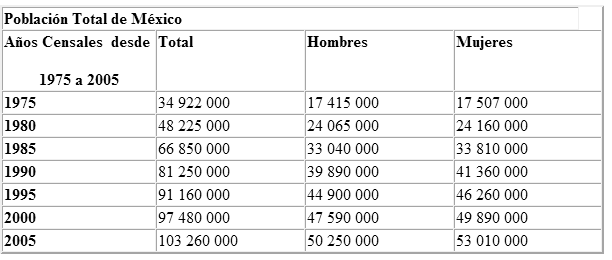
Basado en la siguiente tabla de la población de México contestar las preguntas: 

FUENTE: INEGI. Estadísticas Históricas de México. Censo General de Población y Vivienda


a) Calcule la tasa de crecimiento de las mujeres entre los años 1990 al 2005.


b) Si se sabe que la tasa de crecimiento de los hombres entre los años 1970 al 2000 fue del

200 %, ¿cuál fue la población de hombres en el 1970? (redondee los resultados).


c) En el año 1980 se pensó que la población total de México iba a crecer con un modelo exponencial

de crecimiento continuo. Calcule dicho modelo utilizando los datos disponibles en ese momento, es

decir, 1975 y 1980. Compare los datos para los años siguientes que surgen de ese modelo con los

reales. Interprete los resultados.


Problema 2:

Sea una función definida por


Hallar el conjunto D
Analizar la derivabilidad de
Identificar los intervalos de crecimiento, decrecimiento, concavidad (hacia arriba y hacia abajo), puntos de inflexión, puntos críticos y extremos locales.
Considerar la función en el intervalo [0; 2] y hallar, si existen, extremos globales.





Problema 3

Un hotel necesita contratar un Gerente Comercial y 7 ayudantes. Se presentan a la selección 4 postulantes para la posición de gerente y 10 para la de ayudantes.

Encontrar todas las formas posibles de contratar estas ocho personas.
El hotel cuenta con 4 habitaciones simples, 6 habitaciones dobles y 5 habitaciones familiares todas ellas disponibles para la semana de Pascuas. En dicha semana se realizan 4 reservas para las habitaciones simples, 3 reservas para las dobles y 3 reservas para las familiares. Indicar todas las formas posibles de asignar las reservas.
Una tarde 12 de los turistas alojados organizan un partido de fútbol con dos equipos de 6 jugadores cada uno. Encontrar todas las posibles organizaciones de equipos para el partido.
En este grupo de 12 turistas hay 6 adultos y 6 adolescentes. Se acuerda que cada equipo debe tener al menos 2 adultos. Bajo esta condición ¿de cuántas formas se pueden armar los equipos?



Problema 4

Hallar todas las matrices que verifiquen simultáneamente:

a) es una matriz triangular superior. c)
b) d)




Problema 5

Una fábrica de aceites comestibles produce tres tipos de aceites. Cada uno de ellos es una mezcla que contiene distintas proporciones de uva, girasol y oliva. Se muestran los porcentajes de cada contenido.

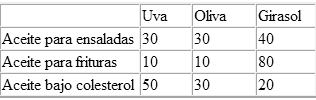
En el Restaurante “Palito’s” se quiere realizar una mezcla de un litro utilizando los tres tipos de aceites con la condición que contenga 34% de Uva, 26% de oliva y 40% de girasol.

¿es posible? (se requiere justificación de la respuesta)
Si la respuesta en a) es afirmativa ¿qué proporción de cada tipo hay que usar?



Problema 6

La ecuación de demanda del nuevo celular-ipod “Apágalo” es de donde se demandan celulares al día cuando el precio unitario es de pesos. El costo total diario de producción de unidades es de pesos donde . Si la producción diaria hoy es de 300 unidades y aumenta a razón de 16 unidades por día, determina la velocidad de cambio de

a) el costo diario total;

b) el ingreso diario total;