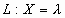 (-1, 0, 1) + (9, 2, -13) y A = (1, 2, -1). Hallar todos los
(-1, 0, 1) + (9, 2, -13) y A = (1, 2, -1). Hallar todos los 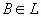 ,
,
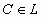 tales que el triángulo ABC sea rectángulo en B e isósceles.
tales que el triángulo ABC sea rectángulo en B e isósceles.Altillo.com > Exámenes > UBA - CBC > Álgebra
|
Álgebra |
1° Parcial |
Tema 4 |
1° Cuat. de 2000 | Altillo.com |
1) Sean 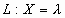 (-1, 0, 1) + (9, 2, -13) y A = (1, 2, -1). Hallar todos los
(-1, 0, 1) + (9, 2, -13) y A = (1, 2, -1). Hallar todos los 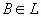 ,
,
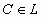 tales que el triángulo ABC sea rectángulo en B e isósceles.
tales que el triángulo ABC sea rectángulo en B e isósceles.
2) Hallar todos los valores de ![]() para
los cuales los sistemas.
para
los cuales los sistemas.
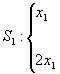
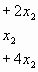
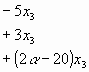
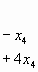
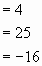
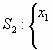
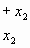
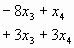
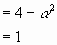
tienen una única solución común. Para alguno de esos valores, hallar la solución.
3) Sean B = 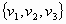 y B’=
y B’=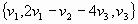 dos
bases del espacio vectorial V. Determinar todos los vectores v de V tales que
las coordenadas de -v en la base B son iguales a las coordenadas de v en la base
B’.
dos
bases del espacio vectorial V. Determinar todos los vectores v de V tales que
las coordenadas de -v en la base B son iguales a las coordenadas de v en la base
B’.
4) Sean los subespacios de 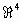 ,
S= <(8, -1, 1, 4) ; (0, 1, 1, 2)> y S’= <(0, 1, 10) ; (4, 1, 2,
3)>.
,
S= <(8, -1, 1, 4) ; (0, 1, 1, 2)> y S’= <(0, 1, 10) ; (4, 1, 2,
3)>.
Hallar W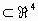 de manera que
de manera que 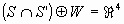 .
.
Para el W hallado, escribir (0,0,0,2) = s + w, con 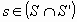 y
y 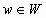 .
.