Altillo.com > Exámenes > UBA - CBC > Álgebra

1.- Sean P = (-1,0,1) , Q = (1,1,2) , R = (1,1,1) y S = (1,2,-1).
Hallar, si es posible, un plano Π tal que d (P,Π) = d (R,Π) = d (S,Π)

2.- Resolver el sistema S para los valores de k para los cuales el subespacio de soluciones del sistema homogéneo asociado a S tiene dimensión 2.

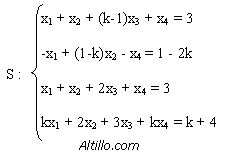
3.- Sean en R⁴ , S = <(1,2,1,0);(1,2,0,-1)> , T = {x Î R⁴ / 2x₁ - x₂ - x₃ + x₄ = x₁ - x₂ + x₃ - x₄ = 0}
Hallar una base se S + T que contenga una base de S y una base de T.
Encontrar, si es posible, s Î S y t Î T de manera que (5,8,3,0) = s + t

4.- Sea {v₁, v₂, v₃} una base de un E.V. V sea B = <-v₁ + v₂ , v₁ +2v₃ , -v₁>
Hallar w Î V para que se verifique simultáneamente:
i) B’ = <2v₂ + v₃ , w , v₁ - v₂> es una base de V.
ii) El vector 4v₁ + v₂ + 2v₃ tiene las mismas coordenadas en las bases B y B’.