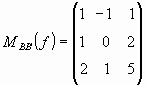Altillo.com > Exámenes > UBA - CBC > Álgebra

1) Sea  f : R³ ® R³ la t.l dada por f(x₁,x₂,x₃) = (x₁+ x₂ , x₁+ x₃, x₁+ x₃). Definir una t.l 
g : R³ ® R³ tal que Nug+ Imf = R³ ; Nuf + Img = R³ y gof (1,1,1) = (1,1,1).

2) Sean V un e.v , B = {v₁;v₂;v₃} y B'= {v₁+v₂+v₃; -v₂+v₃; v₃} bases de V y f  V ® V la t.l. tal que 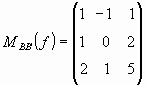Hallar f ^-1 (7v₁+5v₂+8v₃)= {v V / f(v)7v₁+5v₂+8v₃}

3) Hallar todos los a g R para los cuales el polinomio P(x) = x3+ 3ax2-108 tiene una raíz doble. Para alguno de los valores de a hallados , encontrar todas las raíces de P

4. Sea ¦ R3 ®R3 la t.l dada por ¦(x1,x2,x3) = (2x1-x3, 4x2+2x3, 4x1-3x3). Hallar, si existe una base de autovectores de fof.