Altillo.com > Exámenes > UBA - CBC > Álgebra
|
Álgebra |
1° Parcial |
1° Cuat. de 2004 | Altillo.com |
1) Sean Õ : 2x – y + 2z = -8 y L: l (5,-1-8) + (8,-2,14).
Hallar un punto PÎ L tal que d(P,Õ )=9 y determinar el punto Q de Õ más próximo a P.
2) Sean AÎ R3x3, bÎ R3x1 y B=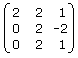 . Se sabe
que
. Se sabe
que
3) Sea B= {v1;v2;v3} una
base de un espacio vectorial V, y sean los subespacios
S= áv1-v2;v1+2v3ñ
, T= áv1+v2;v2+v3ñ
y W= áv1+v2+v3;v2-v3ñ
.
Dar una base {w1;w2} de W tal que w1Î
S; w2Î T y las coordenadas de w1+w2
en base B sean (5,6,4).
4) Sean en R4 los subespacios S= á(1,2,3,0);(0,2,2,1)ñ
y H= {xÎR4
/ 3x1 – x3 + 2x4 = 0}.
Hallar un subespacio W que verifique simultáneamente:
W+S = H; dim(WÇS)
= 1; WÇS^
{0}