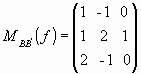
Encontrar v perteneciente a V tal que f(v + v1) = v1.
Altillo.com > Exámenes > UBA - CBC > Álgebra
|
Álgebra |
2° Parcial |
Sede Ciudad | 2° Cuat. de 2004 | Altillo.com |
1) Sea f : R4 à R4
la t.l. dada por:
f (x1, x2, x3, x4) = (x1
– x2, x3 + x4, x1 – x2 –
x3 – x4, - x1 + x2).
Definir si es posible un proyector p: R4 à
R4 tal que p º f = f º
p = 0 R4 y dim(Imp) = 2.
2) Sean B = { v1, v2, v3 } y B` = {v1
– v3, v2, v1 + 2v2}
bases de un e.v. V y f:Và V la
transformación lineal tal que
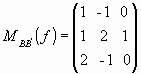
Encontrar v perteneciente a V tal que f(v + v1)
= v1.
3) Sea P(x) = x4 + ax3 + 7x2
– 12x + b. Determinar a y b para que 2 sea raíz doble de
P.
Para los valores hallados, encontrar todas las raíces de P.
4) Sea B = {(1, 0, -1) ; (0, 1, 1) ; (2, 1, 0, )} y f:R3à
R3 la transformación lineal tal que: 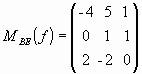 .
.
Encontrar, si es posible, una base B` de R3 tal que M B`
( f ) sea diagonal.