Altillo.com > Exámenes > UBA - CBC > Álgebra
|
Álgebra |
1° Parcial |
1° Cuat. de 2005 | Altillo.com |
En cada ejercicio escriba todos los razonamientos que justifican la respuesta.
1) Sean ∏: 5x – y + z = 1 ; ∏′:
3x + 3y -3z = 7 y L la recta que pasa por (1,-3,0) y (2,-3,2).
Hallar todos los puntos de L que están a igual distancia de ∏ y ∏′
2) Hallar todos los valores de a, b y c para los cuales (1,1,1,-1) es la única solución común de los sistemas S1 y S2
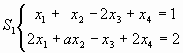
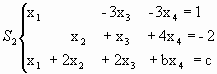
3) Hallar un vector v Є R³ que tenga coordenadas
(3,2,-1) en la base
B = {(1,0,1);(-1,0,1);w} y coordenadas (1,3,1) en la base
B′= {w;(1,1,2);(2,-2,1)}.
4) Sean S= <(2,-1,1,0);(1,0,-3,2)>, H = { x Є R4 /
x1 + x2 –x3 –kx4 = 0} y W = <(0,1,-1,0);(0,3,1,2)>.
Determinar k Є R y un subespacio T incluido W tales que S suma directa T =
H.