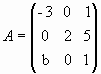 y
y 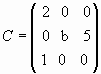 .
.Altillo.com > Exámenes > UBA - CBC > Álgebra
|
Álgebra |
1° Parcial |
1° Cuat. de 2005 | Altillo.com |
1) Sean en R3 los puntos P= (-2,1,4) , Q= (3,1,-2) y la
recta L: λ(2,-1,2) + (7,9,4)
Hallar un plano π que sea perpendicular a L y tal que d(P,π) = d(Q,
π).
2) Sean en R3x3 las matrices las matrices 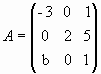 y
y 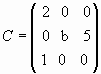 .
.
Encontrar todos los valores de bÎ R para los
cuales el sistema (A + C)x = 2Cx (xÎR3x1)
Tiene infinitas soluciones. Resolver el sistema para alguno de los valores de b
hallados.
3) Sean en R4 S = á(0,2,1,0),(0,2,2,-1)ñ
y T = á(1,0,1,0),(1,0,2,-1)ñ. Hallar, si es
posible, un subespacio W que verifique simultaneamente: w
W Å á(0,2,1,0)ñ = S +
T, (S ÇT) Ì W, W ¹ T
4) Sea S = á(1,0,2,-1),(1,2,0,1)ñ . Hallar si es
posible,una base B={v1;v2;v3;v3
;v4 } de R4 que cumpla las siguientes
condiciones:
i) {v1;v2}sea base de S;
ii) {v3;v4}sea base de S^
;
iii) Las coordenadas del vector (-2,3,-4,2) en la base B sean (0,1,0,1)