Altillo.com > Exámenes > UBA - CBC > Álgebra

En cada ejercicio escriba todos los razonamientos que justifican la respuesta.

1) Sean W = <(0,1,1,-1);(1,-1,0,0);(2,1,0,0)>

S = { x Є R4 / x2 + x3 – x4 = x1 = 0} y T = <(-1,1,0,1);(0,0,1,1)>

Hallar, si es posible, una transformación lineal f: R⁴→R⁴ que verifique simultáneamente:

1. dim(f(W) ∩ S) = 1
2. dim(f(W) ∩ T) = 1
3. Imf = S + T

2) Sean B = {(-2,1,0);(0,0,1);(1,-1,0)} y f: R³→R³ la transformación lineal tal que:

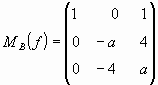
Hallar todos los a Є R tales que f no sea isomorfismo.

Para alguno de los valores hallados dar una base de Nuf y una base de Imf.

3) Hallar todos los z Є C tales que: |3z| = |3z + 8| = 5

4) Sean B = {v1;v2;v3} y B' = {v1 + v2 + v3; v1 – v3; v2 + v3} bases de un e.v. V y sea f: V→V la transformación lineal tal que:

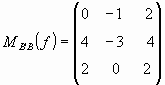
Hallar los autovalores de f y decidir si f es diagonalizable.