Altillo.com > Exámenes > UBA - CBC > Análisis
|
Análisis |
2º Parcial |
Sede Ciudad |
1º Cuat. de 2001 |
Altillo.com |
1- Sabiendo que la función f satisface la ecuación xf ''(x)
+ [f '(x)]3 = e2x para todo ![]() con
f(0) = 4 halle el polinomio de Taylor de orden 3 en x0 = 0 de f.
con
f(0) = 4 halle el polinomio de Taylor de orden 3 en x0 = 0 de f.
2- Encuentre constantes a y b reales tales que  .
.
3- Halle el área de la región del plano ubicada en el primer cuadrante,
comprendida entre los ejes coordenados, la recta ![]() y la curva de ecuación
y la curva de ecuación ![]() .
.
4- Considere la serie de potencias 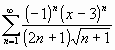 .
Encuentre el intervalo más grande donde la serie converge absolutamente y
estudie la convergencia en los extremos de dicho intervalo.
.
Encuentre el intervalo más grande donde la serie converge absolutamente y
estudie la convergencia en los extremos de dicho intervalo.
Respuestas abajo
Respuestas
1) P3(x) = 4 + x + x²/4 + x³/12
2) a= -8/e y b= 42
3) 1/3 – 1/3 ln(4/3)
4) Converge absolutamente en x=[2;4) y condicionalmente en x=4.