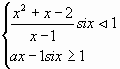1) Si f(x) = 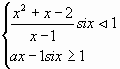es continua para todo x real entonces f(3) es:
a) 4
b) 11
c) 5
d) ninguna de las anteriores

2) Si f(x) = , entonces f tiene puntos críticos en:
a) ¾
b) 1
c) 1 y ¾
d) ninguna de las anteriores

3) es de un gráfico, no te lo puedo mandar, pero es de averiguar un área a partir de la función sen(x)

4) Sea una función continua y biyectiva y sea F una primitiva de f, entonces se puede afirmar que F:
a) es biyectiva
b) es inyectiva
c) es continua
d) ninguna de las anteriores

5) Si una función f tiene un máximo o mínimo local en entonces:
a) f es derivable en y f ´ (a)= 0
b) f tiene un punto anguloso en
c) a es un extremo del dominio de f
d) ninguna de las anteriores

6) Si es una función tal que f(a)> 0 y f(b)< 0 entonces se puede afirmar que:
a) existe por lo menos un tal que
b) existe tal que
c) puede no existir un tal que
d) ninguna de las anteriores

Ejercicio de desarrollo:
7) Sea una función derivable para todo x que tiene un único mínimo local en x=2 y un único máximo local en x=7. Determinar intervalos de crecimiento y decrecimiento, máximos y mínimos de la función , justificando la respuesta.