TOULMIN
Critica a la lógica formal por su análisis y evaluación de argumentos. Dice que la lógica formal por su “autonomía completa” se apartó de las cuestiones sobre cómo analizar y someter a crítica argumentos diferentes.
Él busca ocuparse de los argumentos formulados en el lenguaje ordinario.
Sostiene y postula que su punto de partida es la práctica de la lógica. Opta por una analogía jurídica: la lógica trata del caso que se presenta en defensa de nuestras afirmaciones.
Su investigación consiste en el proceso racional, entendiendo los trámites y categorías que se usan para que las afirmaciones en general puedan ser objeto de argumentación. Es decir, que busca determinar cómo exponer y analizar los argumentos de una manera “lógicamente transparente”. Dice que un argumento sólido es aquel que resiste la crítica.
Para esto plantea un esquema básico:

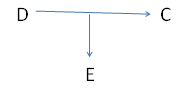
Si se pone en duda una afirmación, quien hizo la afirmación debe justificarla. Primero la debe justificar con hechos que la apoyen mediante la existencia de información documentada. Si se sigue demandando justificación sobre qué tienen que ver los datos dados con la conclusión expuesta, se debe dar información como base que establezca una transición. Es decir no se deben dar nuevos datos, sino que se debe dar reglas, enunciados generales, etc., que evidencien cómo a partir de datos se transita a la conclusión de manera apropiada y legítima.
La garantía es explicativa y su objeto es legitimar la transición. Estas son generales.
Los datos son justificaciones específicas de cada argumento en particular.

Por otra parte Toulmin considera que el esquema de la lógica formal genera una apariencia de uniformidad entre los argumentos, ya que dice que las premisas son los elementos que apoyan a la conclusión.
En cambio en su lógica práctica, permite hacer transparente las diferencia entre:
Premisa singular: que transmite información de la cual se extrae la conclusión.
Premisa universal: que no expone información, sino una garantía o justificación con la que se puede pasar legítimamente del dato a la conclusión.

Toulmin estable un contraste entre:
Argumentos analíticos (llamados teóricos): que no agregan nada al material contenido en las premisas, que intentan fundamentar sus conclusiones en principios universales e inmutables y que son los razonamientos deductivos de la lógica formal. Este argumento es independiente del contexto.
Argumentos sustanciales (llamados práctico): que proporcionan datos o evidencias empíricas para poyar la conclusión del argumento, utilizan argumentos sustanciales que fundamentan sus conclusiones, y son los argumentos prácticos de la vida social. Además son argumentos dependientes del contexto.

CAPITULO CUATRO:
CIENCIAS FORMALES.
Cohen y Nagel dicen que una demostración es una prueba lógica, que no da prueba empírica ni afirma o niega nada acerca de la verdad de las premisas o conclusiones.
En lógica (aritmética y geometría) la verdad de las proposiciones no se demuestran mediante método experimental, sino que en estos casos una prueba lógica es un señalamiento entre un conjunto de proposiciones llamadas AXIOMAS (que no se demuestran) y otras proposiciones llamadas TEOREMAS (que si deben demostrarse).
Desde lo lógico, una demostración puede ser un argumento donde sus premisas son los axiomas o postulados y la conclusión todos sus teoremas deducidos. Esta cuestión lógica tiene que ver con la validez de los razonamientos y afecta al plano sintáctico.
Solo los “vacíos” teoremas deducidos de los axiomas son verdaderos, pero no dicen nada del mundo.

Ciencias formales en la realidad: discusión filosófica.
Popper dice que esa creencia de que los cálculos de la aritmética son aplicables a cualquier realidad es insostenible.
Pero la concepción de las ciencias formales ya se encontraba en Aristóteles que destacaba tres supuestos de la ciencia demostrativa:
El supuesto de la deducibilidad que admite que la ciencia demostrativa debe partir de principios indefinibles (para definir cualquier otro término) y de principios indemostrables o axiomas (para demostrar las verdades de esa ciencia mediante reglas).
El supuesto de evidencia exige que los axiomas sean de una naturaleza que se los pueda aceptar como verdaderos sin demostración. La evidencia debe alcanzar también los términos primitivos para que su claridad permita aceptarlos sin identificación.
Las definiciones son las encargadas de declarar el ser de las cosas y por eso son verdaderas.
Estos dos supuestos admiten al tercero que es el supuesto de la realidad, ya que para Aristóteles “ciencia” siempre es “ciencia de la realidad”.

Los axiomas tienen un carácter general. Los postulados son puntos de partida específicos de cada ciencia.
Ambos, son considerados verdades evidentes que no necesitan demostración. Sobre ellos se demuestra un conjunto de proposiciones que son los teoremas.

La lógica formal es una disciplina que se ocupa de la relación entre las estructuras formales. Una de estas relaciones es la deducibilidad. Una lógica puede ser formal sin ser formalizada. Una lógica esta formalizada cuando se encuentran en ellas los signos no definidos, cuando se enumeran los axiomas usados como premisas y las reglas de razonamiento son consideradas como aceptables, etc.


SISTEMAS AXIOMÁTICOS:
Los componentes son:
1. Los términos primitivos.
2. Las definiciones.
3. Los axiomas.
4. Reglas (razonamientos deductivos).
5. Teoremas.

Peano intenta sistematizar axiomáticamente las verdades conocidas sobre los números naturales, sus propiedades y operaciones básicas.
Los términos primitivos no se definen pero sirven para definir otros términos.
En un sistema axiomático se seleccionan conceptos primitivos o sin definición para definir a partir de ellos otras nociones.
Para construir un sistema axiomático:
Primer paso: proporcionar una lista de los términos sin definición.
Segundo paso: establecer una relación de todas las proposiciones para las que no se dan demostraciones. Estas proposiciones son los axiomas del sistema. Los axiomas se consideran verdaderos sin que su verdad se derive de otros enunciados.
Tercer paso: se realiza lo mismo con los términos, es necesario partir de enunciados que no necesiten demostración para evitar un círculo vicioso.
Cuarto paso: desarrollar el sistema, es decir deducir las consecuencias lógicas mediante reglas de razonamiento deductivo. Estas consecuencias son los teoremas del sistema. Los teoremas son enunciados verdaderos.

Propiedades de los sistemas axiomáticos: debe ser:
Consistente: si desde los axiomas no se puede derivar una fórmula y su negación. Si se admite una contradicción se puede aceptar cualquier enunciado admitiendo que todos son posibles, incluso si se niega y afirma el mismo.
Un sistema inconsistente carece de utilidad, ya que todas las fórmulas pueden ser consideradas teoremas, incluso las que se contradicen.

Independiente: los axiomas deben ser independientes entre sí. Ningún axioma debe derivarse de otro. Si se logra deducir un axioma de otro se prueba que el sistema es redundante y no independiente, pero si se trata de derivarlo y no se logra, no se arma una prueba de que los axiomas sean independientes.

Completo: permite derivar de los axiomas todas las leyes del sistema.

Según Tarski llamamos consistente a una disciplina deductiva cuando no hay en ella dos enunciados que se contradigan o que uno no pueda demostrarse.
La llamamos completa cuando dos proposiciones formuladas, al menos una pueda demostrarse.

GODEL: descubrió que existían afirmaciones verdaderas (teoremas) que no podían ser probadas dentro del sistema. Probó que todo sistema formal que contuviera a la aritmética es incompleto. Descubrió que la consistencia de esos sistemas era imposible de probar.

Interpretación y modelo de los sistemas axiomáticos:
El modelo axiomático es un instrumento de abstracción. Los sistemas axiomáticos actuales son sistemas formalizados, lo que permite que un mismo sistema pueda tener varias interpretaciones. Cada interpretación se denomina un modelo.
Si dos modelos corresponden a un mismo sistema axiomático se dice que son isomorfos. Y si dos modelos son isomorfos, tienen las mismas propiedades formales.