Altillo.com > Exámenes > UBA - Económicas > Análisis II

1_a) Definición de derivada parcial de f (x, y) con respecto a x en (a,b).
    b) Hallar a partir de la definición la derivada parcial con respecto a x de f (x , y) = en (-1,1). Interpretar geométricamente el resultado.
    c) Escribir la ecuación del plano tangente a f en el punto (1,-1,2).

2) Sean y las funciones de demanda de los bienes A y B en función de los precios de cada uno de ellos.
a) Hallar los dominios y representarlos en el plano.
b) Clasificar los bienes.
c) Hallar la elasticidad de ambas demandas con respecto al precio de B cuando e interpretar los resultados.

3_a) Definición de función diferenciable en un punto.
    b) Demostrar que toda función diferenciable en un punto es continua en ese punto.
    c) ¿Usando b) puede hacerse alguna afirmación acerca de la diferenciabilidad en el origen de la función:
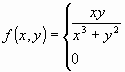   si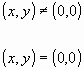   

4) Sea la función de utilidad U(x, y) = .
a) Determinar si es homogenea.
b) Representar en el plano la curva de indiferencia correspondiente a una utilidad igual a 1200. Interpretarla desde el punto de vista económico.
c) Hallar la tasa marginal de sustitución de Y por X cuando x = 4   y = 10 e interpretar el resultado.

5) Sea . Utilizando el diferencial, aproximar el valor de