a) P(A) + P(B) = 1 b)
Altillo.com > Exámenes > UBA - Económicas > Estadística
|
Estadística |
Final |
Tema 2 |
1999 |
Altillo.com |
1) Una población industrial tiene 3 fábricas: A, B y C. Los 40 obreros de
la fábrica A ganan, en promedio $25 por día; los 26 obreros de B, $35 por día
y los 34 obreros de C, $30 por día. El ingreso promedio por día de esa
población industrial es igual a:
a) 30 b) 35
c) 25 d) 29,3
2) Los sucesos A y B son mutualmente excluyentes, entonces
a) P(A) + P(B) = 1 b) ![]() c)
c) ![]() d)
d) ![]()
3) Si x es una variable aleatoria con distribución de Poisson de
parámetro ![]() que
verifica P(x = 58) = 0,5.P (x = 57) entonces
que
verifica P(x = 58) = 0,5.P (x = 57) entonces ![]() es
igual a:
es
igual a:
a) 30 b) 58
c) 29 d) 0,5
4) Un examen consta de 20 preguntas del tipo falso o verdadero. El examen se
aprueba contestando correctamente por lo menos 16 preguntas. Si se lanza una
moneda para decidir el valor de verdad de cada pregunta, la probabilidad de
aprobar el examen es igual a:
a) 0,0013 b) 0,0059 c)
0,9941 d) 0,9987
5) Si Z ~ N (0 , 1) y ![]() entonces
k es igual a:
entonces
k es igual a:
a) 0,41 b) 0,6331 c)
0,44 d) ninguna de las otras es correcta
6) Para la distribución de frecuencias dada por la tabla
|
x |
1 |
2 |
3 |
4 |
5 |
|
f |
5 |
4 |
2 |
4 |
6 |
7) Una urna contiene 3 bolillas numeradas con 1, 2, 3. Se sacan 3 bolillas,
con reposición, y se suman los 3 números. Si la suma de los números es 6,
entonces la probabilidad de que haya salido la bolilla con el número 2 las 3
veces es igual a:
a) 1/3 b)
1/7 c) ½
d) 1/27
8) A y B son dos sucesos que verifican: P(A) = 0,32; P(B) = 0,85; P(B/Ã) =
0,8, entonces P(Ã/B) es igual a:
a) 0,8 b) 0,544
c) 0,2 d) 0,64
9) Si x es una variable aleatoria de distribución binomial de parámetro p,
entonces para n grande, ![]() siendo
siendo
a) ![]() b)
b) ![]()
c) ![]() d)
d) ![]()
10) Si f es la función de densidad de una variable aleatoria X y F es
la función de distribución, entonces ![]() es igual a
es igual a
a) f(2) b) 1 - F(2)
c) 1 - f(2)
d) F(2)
11) Para construir un intervalo de confianza del 95% para el parámetro
binomial p, utilizando una muestra de tamaño n = 120, el valor apropiado de
tabla es:
a) 1,658 b) 1,98
c) 1,645 d)
1,96
12) Para hallar un intervalo de confianza del 95% para una población normal
con ![]() ,
de modo que la media muestral x y la poblacional
,
de modo que la media muestral x y la poblacional ![]() no difieran en mas de 0,6 el tamaño de la muestra debe ser
no difieran en mas de 0,6 el tamaño de la muestra debe ser
a) 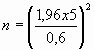 b)
b) 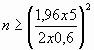 c)
c) ![]() d)
d) 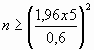
13) Para un test de hipótesis bilateral con un nivel de significación de ![]() ,
la región de aceptación es la región:
,
la región de aceptación es la región:
a) a la derecha del menor valor crítico.
b) a la izquierda del mayor valor crítico.
c) entre los dos valores críticos.
d) fuera del intervalo comprendido entre los 2 valores críticos.
14) Para la serie ![]() ,
se sabe que
,
se sabe que ![]() e
e ![]() .
Una posible ecuación de la recta de regresión de Y sobre X es
.
Una posible ecuación de la recta de regresión de Y sobre X es
a) X = 0,751 + 0,00435y
b) Y = 0,751 + 0,00435x
c) X = 0,00435 + 0,751y
d) Y = 0,00435 + 0,751x
15) Una empresa espera aumentar sus ventas en el año próximo en un 50%. Si
quiere que el ingreso total sea igual al 250% del año anterior, deberá
incrementar los precios en un
a) 66,6% b) 125%
c) 500% d)
166,6%
16) El gráfico de la curva normal para ![]() y
y ![]() es un desplazamiento horizontal del gráfico correspondiente a la curva normal
que tiene
es un desplazamiento horizontal del gráfico correspondiente a la curva normal
que tiene
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
17) A partir de una muestra de tamaño 25 se estimó la esperanza de una
variable aleatoria ![]() ,
con
,
con ![]() desconocido,
mediante un intervalo de confianza del 95% , de longitud 5,3. El desvío
estándar de la muestra fue
desconocido,
mediante un intervalo de confianza del 95% , de longitud 5,3. El desvío
estándar de la muestra fue
a) 6,432 b) 12,864
c) 12,839
d) 6,419
18) En un test de hipótesis unilateral, cuando la hipótesis nula es ![]() la hipótesis alternativa puede ser
la hipótesis alternativa puede ser
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
19) La potencia de un test de hipótesis es de 0,9, entonces para ese test
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
20) El coeficiente de correlación lineal (r) entre X e Y es igual a 0,60.
Entonces la variación total que queda sin explicar por la ecuación de
regresión es del
a) 60% b) 64%
c) 36% d)
40%