Altillo.com > Exámenes > UBA - Económicas > Estadística

1) A: “Después de agrupar un conjunto de datos en cierto número de clases, la mediana es la clase que tiene mayor número de observaciones”.
B: “La varianza es igual a la raíz cuadrada de la desviación estándar”.
Entonces:
a) A es verdadera y B es falsa                     b) A y B son verdaderas
c) B es verdadera y A es falsa                     d) A y B son falsas

2) En una tabla de distribución de frecuencias el ancho de la primera clase duplica al de las restantes. Si al dibujar el histograma, la altura correspondiente a las otras clases es igual a la frecuencia f de cada clase, entonces la altura de la primera clase debe ser igual a:

a)              b)              c)              d) faltan datos

3) La probabilidad de que un valor elegido al azar de una determinada población sea mayor o igual que la mediana es igual a
a) 0,25           b) 0,5             c) 1             d) 0,67

4) A y B son sucesos independientes con y , entonces
a)          b)          c)          d)

5) Una urna tiene 10 bolillas numeradas de 1 a 10. Las bolillas 1 a 4 son rojas, y las 5 a 10 son azules. Se extrae una bolilla, llamamos T: “la bolilla tiene el número 3” y R: "la bolilla es roja”. Entonces.
a) P (T/R) = 0,10               b) P (T/R) = 2/3               c) P (T/R) = 0,25        d) P (R/T) = 0,25

6) X es una variable aleatoria con E(X) = 4. Si Y = 2X + 3, entonces E(Y) vale
a) 11             b) 4             c) 8             d) ninguna de las anteriores

7) La ley de probabilidad de una variable aleatoria discreta está dada por:

Entonces:
a) a = 1/15 y                  b) a = 1/5 y
c) a = 1/15 y                  d) a = 1/5 y

8) En un experimento binomial, sea p la probabilidad de éxito y q la de fracaso. Entonces la probabilidad de obtener x éxitos en n repeticiones es

a)          b)          c)          d)

9) La variable aleatoria x tiene una distribución binomial con media 5 y varianza 4. Se aproxima x por la distribución normal, con corrección por continuidad. Si Z~N (0 , 1) y , entonces k debe ser igual a
a) 0,625         b) 1,25         c) 0,75         d) 1,5

10) En el año 1991 un artículo costaba 25% menos que en 1990. Ese mismo artículo, en 1992, duplicó su valor respecto de 1991. Entonces el número índice del precio de ese artículo, en 1992 tomando a 1990 como base es
a) faltan datos         b) 75         c) 125         d) 150

11) Si f(x) = 2(1 - x) para 0 < x < 1, es la función de densidad de una variable aleatoria continua x, entonces E(x) es igual a
a) ½         b) ¼         c) 1/3         d) 1

12) Sean y Z ~ N (0 , 1), siendo F y G las respectivas funciones de distribución. Entonces siempre se verifica
a)          b)
c)                             d)

13) El promedio de las calificaciones de 30 estudiantes de un curso es 6, con desvío estándar 1,5. Para realizar un intervalo de confianza del 90% para el promedio de las calificaciones debe usar
a) la distribución normal                         b) la distribución t con v = 30
c) la distribución con v = 29             d) la distribución con t = 29

14) Después de tomar una muestra de tamaño n y calcular x, un estadístico dice: “tengo el 88% de certeza de que la media de la población está entre 100 y 120”. Lo que quiere decir en realidad es que
a) la probabilidad de quese encuentre entre 100 y 120 es 0,88.
b) la probabilidad de quesea igual a 110 es 0,88.
c) el 88% de los intervalos calculados a partir de muestras de tamaño n contendrán a la media de la población.
d) ninguna de las anteriores.

15) Sea. En una muestra aleatoria de tamaño 16 se obtuvo x = 130. El intervalo de confianza del 95% paraes
a) (125, 1 ; 134, 9)         b) (81 ; 179)         c) (124, 6725 ; 135, 3275)         d) (125, 8875 ; 34, 1125)

16) Para probar la hipótesis contra , con un nivel de significación, para una población normal con desconocida, se tomó una muestra de tamaño 24. El valor de tabla límite de la región crítica es
a) -1,645         b) -1,711         c) -1,714         d) 1,714

17) Con un menor nivel de significación, la probabilidad de rechazar una hipótesis nula que es realmente cierta
a) disminuye         b) aumenta         c) no varía         d) no se sabe

18) De una población normal con varianza se tomó una muestra de tamaño 25 y se obtuvo una varianza igual a 4900. Se realiza el test contra , para , entonces la región aceptación de es
a) (11, 5 ; 44, 3)         b) (9, 89 ; 45, 6)         c) (10, 9 ; 43, 0)         d) (10, 5 ; 46, 9)

19)

Se sabe que la recta de regresión de Y sobre X es y = 9x + 0,6.

Entonces el valor de k es igual a
a) 18,6                 b) 19                 c) 18                 d) 20

20) Para una serie de datos X e Y se sabe que r = 0,5; 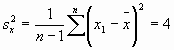      y     . Entonces la pendiente de la recta de regresión de Y sobre X es igual a
a) -1                 b) 0,5                 c) -0,75                 d) 0,75