1) Sea x₁~N(-2;1/4), x₂~X²₃ y x₃~N(0;√5) independientes.
a) Calcular: P(x₂+ x₃²/5<11,143)
b) Calcular: P[(-3≤x₁<2)/(x₁>-2,25)]
2) a) La cantidad de burbujas en un volumen dado de la gaseosa Cochucha sigue una distribución de Poisson de parámetro 1,8. Calcular la probabilidad de que la cantidad de burbujas sea a lo sumo su valor esperado.
b) Un 70% de los clientes de la embotelladora de Cochucha tiene domicilio legal en la ciudad de Buenos Aires (CABA). Si se seleccionan 6 clientes al azar calcular la probabilidad de que no todos tengan domicilio legal en CABA.
3) De los 100 clientes en la embotelladora Cochucha, el 60% son almacenes y el resto son supermercados. El 70% abona sus compras con cheques. Sólo el 12,5% de los supermercados abonan de otra manera.
a) Realizar una tabla de probabilidades conjuntas.
b) ¿Qué porcentaje de los que abonan con cheques son almacenes?
4) Sea una variable aleatoria X que toma sólo los valores -1 y 1. Si su valor esperado es -0,40, elaborar la tabla de probabilidad y calcular P[V(√2-X)≤X<E(1-2X)] justificando claramente su respuesta.
5) Se da a continuación los valores de algunos parámetros obtenidos a partir de 50 observaciones.(completar)
X̄= -50 S²=6,25 P₂₅= -70 P₅₀= -55 P₇₅= -40 mo= -57
a) El valor promedio de la variable es -50, mientras que la mediana es -55. El desvío estándar es 2,5 y el rango intercuartílico es 30.
b) Un 75 % (porcentaje) de las observaciones superan el valor -70 y hay 25(cantidad) observaciones que superan el valor -55.
c) Una observación que toma el valor -120 ¿es atípica severa, atípica moderada o no atípica? Justifique su respuesta.
Respuestas:
1)a)P(x₂+x₃²/5<11,143)=
↓por complemento
= 1-P(x₂+x₃²/5≥11,143)= *Dado que x₂:X²₃ y x₃: N(0;√5)
↓busco en la tabla de la chi cuadrado x₃/√5: N(0;1) → (x₁/√5)²: X²₁
= 1-0,025=0,975 →(x₃/√5)²+x₂= x₂+x₃²/5:X²₄
b)P[(-3≤X₁<-2)/(X₁>-2,25)]=
P[(-3≤X₁<-2) ∩ (X₁>-2,25)] / P(X₁>-2,25)
/ P(-2,25<X₁<-2) =
P(X₁>-2,25) Estandarizo, X₁:N(-2;174) / P(-1<Z₁<0) =
p(Z₁>-1) / F(0)-F(-1) =
1-P(Z₁≤-1) / F(0)-[1-F(1)] =
1-F(-1) / F(0)-[1-F(1)] =
1-[1-F(1)] / F(0)-1+F(1) =
1-1+F(1) / F(0)-1+F(1) =
F(1) / 0,5-1+0,8413 = 0,4057
0,8413
2) a) Datos:
X: La cantidad de burbujas en un volumen dado de la gaseosa Cochucha.
X:P(1,8) λ=E(X)=1,8
P(X≤1,8)=P(0)+P(1)=0,1653+0,2975=0,4628
b)X: Cantidad de clientes de la embotelladora Cochucha.
*Una forma es tomar como p( probabilidad de éxito) a que un cliente tenga domicilio legal en CABA.
Entonces p=0,70(el dato)
X~Bi(6;0,70)
P(x<6)=1-P(X≥6)= 1-0,1176= 0,8824
*Otra forma es pensar que p es la probabilidad de que un cliente de la embotelladora no tenga domicilio legal en CABA.
Entonces p=0,30
X:Bi(6;0,30)
P(X≥1)=1-p(X=0)=1-0,1176=0,8824
3) a) Sucesos:
A: La cantidad de clientes que son almacenes.
S: La cantidad de clientes que son supermercados.
C: La cantidad de clientes que abonan con cheques.
O: La cantidad de clientes que abonan con otra forma de pago.
Datos:
P(A)=0,60
P(C)= 0,70
P(O/S)=0,125
Tabla de probabilidades conjuntas:
|
A |
S |
Total |
|
|
C |
0,35 |
0,35 |
0,70 |
|
O |
0,25 |
*0,05 |
0,30 |
|
Total |
0,60 |
0,40 |
1 |
*P(O/S)=P(O ∩ S)/P(S)
0,125= P(O ∩ S)/0,40
0,125.0,40= P(O ∩ S)
P(O ∩ S)=0,05
a) P(A/C)= P(A ∩ C)/P(C)=0,35/0,70=0,50
Rta: El 50% de los que abonan con cheques son almacenes.
4) a)
Datos:
|
X |
P(X) |
E(X)= x. p(x) |
|
-1 |
a |
-a |
|
1 |
1-a |
1-a |
|
1 |
-0,40 |
E(x)= -a+(1-a)
E(x)= -2a+1
-0,40= -2a+1
-1,40= -2a
-1,4/-2= a
a= 0,70
Tabla de probabilidad
|
x |
P(x) |
x² |
E(x²) |
|
-1 |
0,70 |
1 |
0,70 |
|
1 |
0,30 |
1 |
0,30 |
|
1 |
1 |
b)
ü V(X)=E(X²)-E(X)²
V(X)=1-(-0,40) ²
V(X)= 1-0,16
V(X)=0,84
ü P[V(√2-X)≤X<E(1-2X)]=
P[V(-X)≤X<1+E(-2X)]= propiedades aplicadas: V(X+k)= V(X) y E(X+k)=E(X)+k
P[(-1)²V(X)≤X<1-2E(X)]= propiedades aplicadas: V(kX)=k²V(X) y E(kX)=kE(X)
P[V(X)≤X<1-2E(X)]=
P[0.84≤X<1-2.(-0,40)]= Datos: V(X)= 0,84 y E(X)= -0,40
P[0,84≤X<1-(-0.80)]=
P(0,84≤X<1,80)= La variable x toma el valor 1 y -1 únicamente, y dentro de
P(X=1)=0,30 ese rango se encuentra el valor 1. La p(1) sale de la tabla del punto a).
5) c)
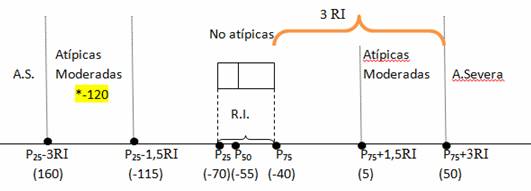
Rta: La observación que toma el valor -120 es atípica moderada.