Altillo.com > Exámenes > UBA - Farmacia y Bioquímica > Física
| Física | Trabajo Práctico: Calibración de un Tensiómetro | 2006 | Altillo.com |
CALIBRACIÓN DE UN TENSIÓMETRO
OBJETIVOS:
Calibrar el tensiómetro, asignar a la escala que posee unidades de masa o de fuerza.
FUNDAMENTO:
Experiencia basada en los principios de la calibración. Un material de masa conocida es suspendido del anillo que cuelga del brazo lateral, se observa la división del tensiómetro, que indica la tensión ejercida del brazo lateral al llegar a la posición horizontal.
MATERIALES:
Balanza analítica
Tensiómetro
Pesas de prueba
Pinza.
MÉTODO:
Pesar las pesitas de prueba con balanza analítica y anotar los datos obtenidos.
Poner en cero el tensiómetro, esto se logra al suspender el anillo del extremo del brazo lateral y modificar la torsión del alambre hasta que el brazo lateral se encuentre en posición horizontal. En este punto, hacer coincidir el cero de la escala principal del tensiómetro con la escala del vernier que tiene adjunto.
Colgar del anillo las pesas de masa conocida. Torsionar el alambre hasta retornar el brazo a la posición horizontal y efectuar la lectura del indicador en la escala. Anotar los datos obtenidos.
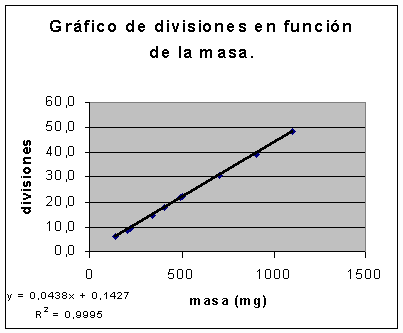
Realizar un gráfico que relacione las divisiones del tensiómetro con la masa de las pesas suspendidas en cada lectura.
DATOS:
Incerteza de la balanza analítica = +_1mg
Aproximación de la escala del tensiómetro = +_0,1
RESULTADOS:
Tabla de divisiones del tensiómetro en función de la masa de las pesas suspendidas en cada lectura:
| Divisiones(+_0,1) | Masa(mg)(+_1mg) |
| 5,9 | 137 |
| 8,8 | 200 |
| 9,2 | 215 |
| 14,9 | 337 |
| 17,7 | 400 |
| 22,0 | 493 |
| 22,6 | 500 |
| 31,0 | 700 |
| 39,3 | 900 |
| 48,0 | 1100 |
DISCUSIÓN:
Del gráfico sacamos la relación entre divisiones y masa (mg), de esta manera calibramos el tensiómetro asignando a su escala unidades de masa. Pasamos la masa a gramos, y con m, la pendiente de la recta de nuestro gráfico (que es la relación entre las divisiones y la masa), hicimos la conversión de unidades de masa (gramos) a unidades de fuerza (dinas). De esta manera logramos calibrar al tensiómetro asignándole a su escala unidades de fuerza, mas apropiadas para la medición de tensiones.
GRÁFICO:

TERMÓMETRO DE MERCURIO.
OBJETIVO:
Verificar la escala del termómetro.
FUNDAMENTO:
Determinación de la temperatura de ebullición del agua a la presión del día mediante la ecuación de Clausius_Clapeyron, la cual tiene en cuenta como afectan los cambios de presión a la temperatura de ebullición del agua. Nos basamos en las leyes de cambios de fases, a saber, que la temperatura se mantiene constante durante todo el proceso de cambio de fase, y que los puntos de fusión y ebullición son característicos de cada sustancia.
A partir del diagrama de fases del agua, se ve que los cambios de presión alteran significativamente la temperatura de ebullición, y no así la de fusión, que permanece casi constante a pesar de cambios notables de presión.
MATERIALES:
Termómetro de mercurio
Mechero
Balón con salida lateral
Agua
Recipiente con agua y hielo.
MÉTODO:
Colocar el termómetro en un recipiente donde coexisten los estados sólido y líquido del agua, y cuando se estabilice la columna de mercurio leer la división alcanzada, determinar la temperatura de fusión del agua a la presión atmosférica del momento.
Colocar el termómetro en un balón con salida lateral en el que se encuentre agua en ebullición, de manera que el bulbo este en contacto con el vapor. Determinar la temperatura de ebullición en las condiciones experimentales mediante la lectura de la división alcanzada por la columna de mercurio una vez estabilizada.
Calcular mediante la ecuación de Clausius_Clapeyron la temperatura de ebullición a la presión atmosférica de la experiencia.
Calcular alfa, la relación entre los grados exactos e inexactos mediante la siguiente expresión:
Alfa= te / (t100 - t0).
DATOS:
Presión del día= 753,62 mmHg
Temperatura de fusión del agua _tf = 0ºC
RESULTADOS:
Temperatura de fusión_ t0 = (0+_1)ºC
Temperatura de ebullición_ t100 = (100+_1)ºC
Temperatura de ebullición según ecuación de Clausius_Clapeyron (dato teórico)_ teb= 99,76ºC
Alfa= 0,9976
CONCLUSIÓN:
Con los resultados obtenidos y los datos teóricos determinamos si la escala del termómetro estaba bien armada o no. Lo hicimos por comparación entre los grados exactos (es decir la diferencia entre los valores teb y tf que son teóricos) y los grados inexactos (es decir la diferencia entre los valores experimentales t100 y t0 ). Si la escala del termómetro estuviera perfectamente construida, la relación entre los grados exactos e inexactos (alfa) debería dar 1. De esta manera asignamos a las divisiones del termómetro valores de la cantidad de grados que representan. El hecho de que alfa nos haya dado menor que 1 nos da la pauta que la escala del termómetro esta estirada, ya que los grados inexactos son mayores que los exactos.
A fines prácticos, si quisiéramos saber el valor real de lo que medimos, deberíamos multiplicar el valor leído por alfa. De todos modos, en el caso de un termómetro como el que utilizamos en esta experiencia, esto no tiene sentido, ya que alfa nos dio muy cercano a 1 y el termómetro tiene una aproximación de 1ºC, por lo cual esas pequeñas diferencias no se podrían visualizar en la escala. Tras este análisis, llegamos a la conclusión de que el termómetro que usamos es poco sensible pero muy confiable, gracias al valor de alfa, tan cercano a 1 que obtuvimos.