Altillo.com > Exámenes > UBA - Psicología > Estadística

1) Un investigador quería demostrar que existían diferencias entre varones y mujeres de 12 años de edad en cuanto al número de adjetivos que emplean en una conversación. Preparó un experimento en el cual grabó las conversaciones de 8 varones y de 10 mujeres y halló que el promedio de la cantidad de adjetivos usados por las mujeres era de 18 adjetivos por hora con una desviación estándar de 5 adjetivos. Para los varones el promedio era de 12 adjetivos con una desviación estándar de 3 adjetivos. Pudo el investigador demostrar su hipótesis? Utilice el nivel de riesgo del 1% para responder a la pregunta.

2) Los trastornos de personalidad son bastante comunes. Los datos epidemiológicos sugieren que afectan al 10% de la población. Sin embargo, solo la mitad de los afectados concurre a un tratamiento psicológico. 
a) ¿Cuál es la probabililidad de que entre cinco personas tomadas al azar de la población, ninguna padezca trastorno de personalidad?
b) Si trabajo en una institución psiquiátrica, cuál es la probabilidad de que entre diez personas que pidieron consulta para hoy, haya por lo menos un caso de trastorno de personalidad?

3) Suponiendo que el ingreso salarial de las familias argentinas sigue un modelo normal, en el hipotético caso que el ingreso promedio sea de $700 y el desvío de $300:
a) Calcule el porcentaje de la población que gana por debajo de $400
b) Calcule el mínimo ingreso de las familias del 2% más adineradas.

PREGUNTAS TEORICAS
1) Explique las características de una distribución binomial y sus condiciones.
2) Enuncie y explique el teorema central del límite.

Respuestas

1) Contraste de Hipótesis con dos variables y δ conocido.
Ho: μ1 = μ2
H1: μ1 ≠ μ2

Datos:
x1 = 12
x2 = 18
S1= 3
S2 = 5
Μ = 12
δ = 3
α = 0.01
gl = (n1 + n2 – 2) = 16
área: 0.995
t = 2.921

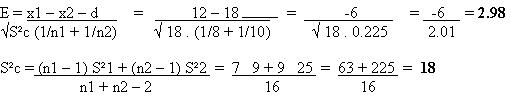
El investigador pudo demostrar su hipótesis ya que el estadístico de contraste cae en una zona de rechazo. Por lo tanto, a un nivel de riesgo del 1% descartamos la Hipótesis Nula y proponemos la H1.

b) n = 10
π = 0.05
P (x >= 0) = f1 + f2 + f3 +…+ f10 = 0.315+0.075+0.010+0.001 = 0.401

3) Distribución Normal.
a) X = 700
S = 300
P (x < 400)
P (z < -1) = 0.1587
El porcentaje de la población que gana por debajo de $400 es el 15.87 %

b) x = 700
S = 300
área: 0.02, 1 – 0.98 = 2.07 = z
x = x + z . S (destipificación)
x = 700+ +2.07 . 300
x = 1.321
El ingreso mínimo de las familias más adineradas es de aprox. $1.321

Es la repetición de n experiencias, con una probabilidad de éxito constante, donde , cada una de ellas dicotómicas (valor éxito – no éxito). Si se cumplen estas condiciones, podemos trabajar con la distribución binomial.
π de éxito - π de no éxito = 1
π de éxito = 1 – π de no éxito.

2) Prueba de hipótesis. Las medias de las medias grupales da un valor cercano a μ (media grupal) con una desviación de la enésima parte del desvío poblacional (δ). Su utilidad radica en realizar inferencias a partir de las conclusiones o propiedades de una muestra acerca de una población, a la que quiere representar.