1) Sean las rectas
![]()
a. Halle
![]()
b. Si a=0, calcule la distancia entre ambas rectas
2) Sea la superficie
![]()
a. Halle todos los A,B,C![]() ,
tales que la superficie sea:
,
tales que la superficie sea:
i. Cilindro circular recto de eje paralelo al eje x.
ii. Hiperboloide de una hoja de eje paralelo al eje z tal que su traza con el plano z=0 sea una elipse de eje focal paralelo al eje x, cuyo semiejes tengan longitudes 3 y 4.
b. Para A=1, B=C=-1, identifique y grafique la superficie.
3) Sea la transformación lineal :
![]()
a. Halle todos los
![]() tales
que T no sea un monoformisfo (T no sea inyectiva).
tales
que T no sea un monoformisfo (T no sea inyectiva).
b. Para a=0, halle N(T), Im(T), bases de cada uno y verifique el teorema de las dimensiones.
4) Analice el valor de verdad de cada una de las siguientes afirmaciones, justificando su respuesta:
a. Sea una transformación lineal T:V![]() W
W
i. Si dimV=5 y dimW=3 entonces dimNu(T)=2
ii. Si V y W tienen dimensión finita y Nu(T)=V entonces Im(T)=![]()
b. Sea A=![]() un
conjunto de vectores L.I. (linealmente independiente)
un
conjunto de vectores L.I. (linealmente independiente)![]()
![]()
5) Sea la ecuación
![]() en R2
en R2
a. Halle todos los valores de
![]() tales
que la ecuación corresponda a una hipérbola.
tales
que la ecuación corresponda a una hipérbola.
b. Para k=3, identifique y grafique la curva.
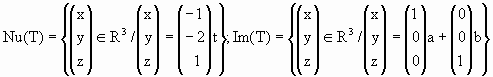
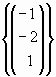 ,
una base de la imagen
,
una base de la imagen
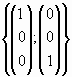
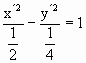 hipérbola con centro en el origen y eje focal y=x
hipérbola con centro en el origen y eje focal y=x